Xn=3n/n+1 Найти:
1)Член x1; x4;x9;x99;x999.
2)Определить вырастает или убывает последовательность.
3) Определить ограниченность.

Другие вопросы по теме Математика
Популярные вопросы
- На рисунке показано как измерили массу пустой мензурки, мензурки с жидкостью...
2 - Примером образной информационной модели является: 1.схема2.график3.формула4.рисунок...
1 - Контрольные вопросы к главе 2...
3 - Вычисли :А/4 :5 :А /10=/=Дробная черта ...
2 - Школа лэнли это??? Вот из этих ответов надо выбрать правельный: а) в Лондоне,...
2 - 1)Найдите значение выражения 25а2 при а=-5 2)раскройтк скобки и найдите значение...
3 - один вопрос Фактор, увеличивающий седиментационную устойчивость суспензий а)...
3 - Известно, что треугольники подобны, и их площади относятся как 81100. Как относятся...
2 - Задание № 6. Выбрать правильные ответы. (2 верных ответа). В процессе перемещения...
2 - Мына тапсырманы ким биледи комектесиндерши...
3
1) x₁ = 1,5; x₄ = 2,4; x₉ = 2,7; x₉₉ = 2,97; x₉₉₉ = 2,997;
2) строго возрастает;
3) ограничена.
Пошаговое объяснение:
1)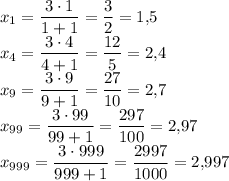
2) Оценим разность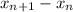 :
:
Поскольку n ≥ 1 (как натуральное число), n + 2 > 0, n + 1 > 0. Тогда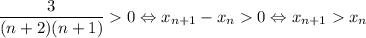 — каждый следующий член строго больше предыдущего, значит, последовательность строго возрастает.
— каждый следующий член строго больше предыдущего, значит, последовательность строго возрастает.
3) Поскольку последовательность строго возрастает, она ограничена снизу первым членом. Проверим ограниченность сверху:
Последовательность ограничена сверху. Поскольку она ограничена и сверху, и снизу, то она ограниченная.