1. Математика
  2. X²-7x:5+2x=2 хелпаните срч

X²-7x:5+2x=2 хелпаните срч

Даша333555 Даша333555    3   09.01.2022 14:07    2

Ответы
321Shark 321Shark  09.01.2022 14:10

x_{1} ≈ -1,74568 ; x_{2} ≈ 1,14568

Пошаговое объяснение:

1. Запишим деление в виде дроби

x²-7x:5+2x=2 = x²-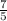\frac{7}{5}x+2x=2

2. Вычислим сумму

x²-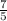\frac{7}{5}x+2x=2 = x²+\frac{3}{5}x=2

3. Умножаем обе части уравнения на 5

x²+\frac{3}{5}x=2 = 5x²+3x=10

4. Переносим константу в левую часть и изменяем её знак

5x²+3x=10 = 5x²+3x-10=0

5. Решаем квадратное уравнение ax²+bx+c=0 используя {

x =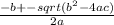 \frac{-b +- sqrt(b^{2}-4ac)}{2a}

} :

x =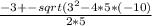 \frac{-3 +- sqrt(3^{2}-4*5*(-10)}{2*5}

6. Вычисляем степень

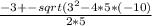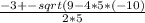
x=\frac{-3 +- sqrt(3^{2}-4*5*(-10)}{2*5} = x=\frac{-3 +- sqrt(9-4*5*(-10)}{2*5}

7. Вычисляем произведение

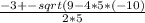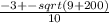
x=\frac{-3 +- sqrt(9-4*5*(-10)}{2*5} = x=\frac{-3 +- sqrt(9+200)}{10}

8. Сложим числа

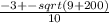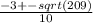
x=\frac{-3 +- sqrt(9+200)}{10} = x=\frac{-3 +- sqrt(209)}{10}

9. Запишим решения: одно со знаком + и одно со знаком -

x=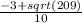\frac{-3 + sqrt(209)}{10}

x=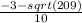\frac{-3 - sqrt(209)}{10}

10. Уравнение имеет 2 решения

x_{1}=\frac{-3 + sqrt(209)}{10}

x_{2}=\frac{-3 - sqrt(209)}{10}

11. Решение

x_{1}=\frac{-3 + sqrt(209)}{10}

x_{2}=\frac{-3 - sqrt(209)}{10}

=

x_{1} ≈ -1,74568

x_{2} ≈ 1,14568

ПОКАЗАТЬ ОТВЕТЫ
динозаврррррр динозаврррррр  09.01.2022 14:10

≈ -1,74568 ;  ≈ 1,14568

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
2880905 2880905  23.06.2019 19:30
Как по китайский слова я тебя люблю...
58624789485 58624789485  23.06.2019 19:30
Реши . туристы были в пути пать суток десять часов . на самолете они летели 18 часов . на поезде ехали на 32 часа больше,чем летели . остольное время туристы плыли на...
daniil12341234 daniil12341234  23.06.2019 19:30
Решить. известно,что х и у -положительные числа.сравните -а) 0 и х б) -у и 0 в) -х и у г) у и -х д),/х/ и -х е) /у/ и у ж) -х и /-у/ з)/х/ и -у...
Маратрмл Маратрмл  23.06.2019 19:30
Вырвжение: 1)3a-4c+11a-6c; 2) -3x*(-2y)....
roman19781975 roman19781975  23.06.2019 19:30
Всервисе отремонтировали 40 моторов автомобилей и мотоциклов. сколько отремонтировали авто и мото, если из сервиса вышло 100 колес...
Adriet Adriet  23.06.2019 19:30
Составь решение которой является следующее выражение: 9+(12-7) записать решение этой по действиям и вычисли ответ. нужно соствить краткую запись...
Анастасия23102002 Анастасия23102002  23.06.2019 19:30
Собрали 9 600 кг картофеля и 6 400 кг моркови. картофеля получилось на 80 мешков больше, чем моркови. сколько было мешков картофеля и сколько моркови? один маляр работал...
sargsyantatev1 sargsyantatev1  23.06.2019 19:30
Реши для ремонта школы 900 штук белых и красных кирпичей ,одинаковых по массе . масса всех красных кирпичей 1900 кг , а масса белых 1700 кг . найди количество красных...
gagag590 gagag590  23.06.2019 19:30
В9каробках 3690 ручек а в 8 4720 карандашей узнай чего больше в одной коробке ручек или карандашейи на сколько...
neketapro neketapro  23.06.2019 19:30
Решить ! маша и алёша вышли из своих домов, расположенных на одной улице, и пошли навстречу друг к другу. маша шла до места встречи со скоростью 65 м/мин и метров. алёша...

Популярные вопросы