(x-3)^2(4+x)/(1+x)(x-6)^3 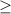 0 36/x^2-5x
0 36/x^2-5x 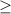 x^2-5
x^2-5
C подробным решением
Другие вопросы по теме Математика
Популярные вопросы
- Вычислите скалярное произведение векторов p = a-b-c и q = a-b + c, если а = 5,...
2 - Докажите, что треугольник с вершинами А (3; 0), В (1; 5) и С (2; 1) тупоугольный....
3 - Найдите площадь треугольника ABC, если ВС = 41 м, ∠A = 32°, ∠C = 120°...
1 - Постройте угол В, если sin В = 1/2...
2 - Теорема об отношении периметров подобных многоугольников...
1 - Постройте угол А, если cos А = - 3/4...
1 - Точка D — середина отрезка NK, длина которого равна 2. Найдите множество всех...
1 - Даны координаты вершин трапеции ABCD: А (-2; -2), В(-3; 1), С (7; 7), D (3; 1)....
3 - Точка В — середина отрезка АС, длина которого равна 2. Найдите множество всех...
1 - Постройте окружность, заданную уравнением (х + 5)2 + (у - 3)2 = 25....
1
1. x ∈ (-∞; -4]∪(-1; 6)∪(6; +∞)
2. x ∈ (-∞; -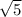 ]∪(0;
]∪(0; 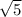 )∪(5; +∞)
)∪(5; +∞)
Объяснение:
1. (x-3)^2(4+x)/(1+x)(x-6)^3 ≥0
Приравниваем функцию к нулю:
(x-3)^2(4+x)/(1+x)(x-6)^3=0
x = 3
x = -4
x ≠ -1
x ≠ 6
Строим числовую ось и отмечаем промежутки возрастания/убывания. Подойдут только те, где х больше либо равен 0.
ответ: x ∈ (-∞; -4]∪(-1; 6)∪(6; +∞).
2. 36/x^2-5x≥x^2-5
36 / (x (x - 5) (x^2 - 5)) ≥ 0
Приравниваем функцию к нулю:
36 / (x (x - 5) (x^2 - 5)) = 0
x ≠ 0
x ≠ 5
x ≠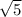
x ≠ -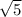
Строим числовую ось и отмечаем промежутки возрастания/убывания. Подойдут только те, где х больше либо равен 0.
ответ: x ∈ (-∞; -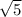 ]∪(0;
]∪(0; 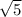 )∪(5; +∞)
)∪(5; +∞)