1. Математика
  2. X² = 2x+8Можно решение подробное?)

X² = 2x+8
Можно решение подробное?) ​

krasnov595egr krasnov595egr    3   27.08.2020 23:23    0

Ответы
katunina2004ox971p katunina2004ox971p  15.10.2020 16:23

Квадратное уравнение.

Можно предположить, что корня ровно два и оба действительные (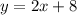y = 2x+8 находится выше точки (0;0), а у параболы 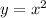y=x^2 ветви направлены вверх и минимум в точке (0;0), поэтому прямая 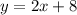y=2x+8 пересекает обе ветви параболы).

Найдем корни.

x^2 = 2x+8

x^2 -2x - 8 = 0

D = (-2)^2 -4 \cdot 1 \cdot -8 = 4 + 32 = 36 0

x_1 = \frac{-(-2)+\sqrt{36}}{2 \cdot 1} = \frac{2+6}{2} = 4

x_2 = \frac{2-6}{2} = -2

ответ: x1 = 4; x2 = -2.

============================

Если решение устроило, не забудь отметить его как "Лучшее".

ПОКАЗАТЬ ОТВЕТЫ
shepa174 shepa174  15.10.2020 16:23

ответ: корни -2 и 4. См фото.

Пошаговое объяснение:


X² = 2x+8Можно решение подробное?) ​
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
cimuzoro cimuzoro  07.07.2019 12:20
Решить логическую . в группе 15 детей . 10 детей любят мороженое , 9 человек конфеты . как это может быть...
LalkaDestroyer LalkaDestroyer  07.07.2019 12:20
Фигуры вырезали из бумаги.из красной из синей из серой и положили на стол так чтобы они частично закрывали друг друга.придумай 6 вариантов расположения заполни таблицу фигурами...
denholopДанила23231 denholopДанила23231  07.07.2019 12:20
А) х-3.5=2х-1; б) 0.4 целых икс=2 целых 3...
victoria223 victoria223  07.07.2019 12:20
5учеников купили 100 тетрадей, кирил и витя купили 52 тетради, витя и юра -43 юра и сева-34 сева и миша -30 сколько тетрадей купили каждый из них...
vanyaver vanyaver  07.07.2019 12:20
Решить логическую . как с 5 литровой кастрюли и 3 литровой банки налить из водопроводного крана в ведро ровно 4 л . лишнюю воду можно выливать ....
Перуна Перуна  07.07.2019 12:20
Пятерку на контрольной работе получили 3 ученика, четверку на 6 больше, чем пятерку, тройку на 8 больше, а двойку на 6 меньше, чем четверку. сколько учеников писали контрольную...
gladishsofiya gladishsofiya  07.07.2019 12:20
Длинна отрещка вс-6см длина оирезка мn-2см5мм на сколько доинна первого отрезка болтге второго...
адрдрюе адрдрюе  07.07.2019 12:20
(127+х)-236=418 (492-а)-87=245 (y-246)+154=300 745-(b-358)=455 решите...
kondakovvasenk kondakovvasenk  07.07.2019 12:20
Запишите пары чисел ,в которых второе число кратно первому ; 1)5 и 45 2)9 и 71 3)8 и 34 4) 16 и 80 5)17 и 51 6)4 и 63 7)12 и 60 8)23 и 115...
Катя7544 Катя7544  07.07.2019 12:20
Найти значение квадратичной функции y=5x+5x+2x-7 при x=1; -2...

Популярные вопросы