(x^2-a(a+1)x+a^3)/√(2+x-x^2)=0
когда уравнение имеет 2 разных корня
Другие вопросы по теме Математика
Популярные вопросы
- Общие признаки треугольника. нужно . не признаки равенства, а общие...
2 - My summer holidays ! только не из интернета и чуть чуть про экспо в...
3 - ответ (необезательно) главное по дейсвиям : (4750: 19-40*13)*(1234*4321-1999)+5...
3 - Проба пера придумай рассказ друзя в беде...
1 - :77777777=700; 22222222=200; 4444444444=500; 6666666666=600 9999999999=1000...
3 - Всборнике 80 сказок из них 13 сказок про животных небылиц на 7 на 17...
3 - Золким ранкам па расе выйшла сонца да вады.пахавалися мы усе.а шукаць...
2 - Нужно выписать из текста 3 предложения. сложно подчиненное, бессоюзное...
2 - Стороны основания прямого параллелепипеда равны 3 м и 9 м, а его диагонали...
1 - Нужно составить вопрос . из этих предложений. 1 оның үстіне əпкесі...
3
Решение: Запишем ОДЗ:
Переходим к уравнению-следствию: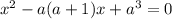 .
.
Найдём дискриминант:![D=[-a(a+1)]^2-4\cdot1\cdot a^3=a^4+2a^3+a^2-4a^3=a^4-2a^3+a^2=a^2(a^2-2a+1)=a^2(a-1)^2=[a(a-1)]^2.](/tpl/images/2005/6762/e07c3.png)
Дискриминант при любых значениях параметра, а значит квадратное уравнение всегда имеет корень. При
при любых значениях параметра, а значит квадратное уравнение всегда имеет корень. При  дискриминант равен 0 и уравнение имеет единственное решение. Такой вариант нас не устраивает, поэтому будем рассматривать все
дискриминант равен 0 и уравнение имеет единственное решение. Такой вариант нас не устраивает, поэтому будем рассматривать все 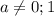 . Для них квадратное уравнение имеет два корня:
. Для них квадратное уравнение имеет два корня:
Чтобы исходное уравнение имело два корня необходимо, чтобы оба корня удовлетворяли ОДЗ, т.е.
Не забудем исключить 0 и 1 из данного промежутка значений и получим окончательный ответ.
ОТВЕТ: при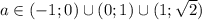 .
.