1. Математика
  2. Взале клуба столько рядов, сколько

Взале клуба столько рядов, сколько мест в каждом ряду. если число рядов увеличить в два раза и уменьшить на 10 количество мест в каждом ряду, то число мест в зале увелисится на 300. сколько радов в зале?

Domashkafu Domashkafu    2   15.03.2019 13:30    1

Ответы
yukodraw yukodraw  25.05.2020 12:55

Пусть x - число рядов;

         y  - число мест в ряду;

         z - общее число мест.

Составис систему уравнений для двух ситуаций:

\left \{ {{x*y=z} \atop {2x*(y-10)=z+300}} \right.

учитывая, что x=y  по начальному условию задачи, то система уравнений приобразуется в

\left \{ {{x^{2}=z} \atop {2x*(x-10)=z+300}} \right.

заменим z во втором уравнении на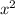 x^{2} из первого. Тогда получим:

2x*(x-10)=x^{2}-300

расскрываем скобки и решаем квадратное уравнение:

2x^{2}-20x=x^{2}+300 </p&#10;<px^{2}-20x-300=0 </p&#10;<pD=400+1200=1600 </p&#10;<px1=\frac{20+40}{2} </p&#10;<px1=30 </p&#10;<px2=\frac{20-40}{2} </p&#10;<px2=-10 

так как количество рядов не может быть отрицательным числом, то второй корень не подходит. Следовательно ответ: 30 рядов.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
emeli2007 emeli2007  29.07.2019 17:00
Сколько будет рублей если у тебя 20000 капеек...
alenabovkun alenabovkun  29.07.2019 17:00
Начерти прямоугольник со сторонами 3 см и 2см найди его площадь в квадратных сантиметрах и выразил её значение в квадратных милиметрах...
zlatakadochnik zlatakadochnik  29.07.2019 17:00
Составит на эти решение 3*6=18. 18 -5=13....
Ожзвэ Ожзвэ  29.07.2019 17:00
:за 5 кг яблоки и 5 кг абрикосов заплатили 600 рублей. абрикосы дороже яблок в 2 раза . какова цена абрикосов и цена яблок...
Мария31011 Мария31011  29.07.2019 17:00
:длина прямоугольника 3см. чему равна ширина , если периметр 10 см?...
Rina666 Rina666  29.07.2019 17:00
Сколько процентов срставляет числр 13 от 100?...
batkia228 batkia228  29.07.2019 17:00
Винтик и шпунтик подтянулись вместе 36 раз причем винтик подтянулся на 14 раз меньше шпунтика. сколько раз подтянулся каждый из них. незнайка и кнопка играли в игру....
ilonka20048 ilonka20048  29.07.2019 17:00
Решить 3 класс велосипедист двигался 3 ч. со скоростью 15 км/ч и проехал за это время 1 3 -дробь всего расстояние. с какой скоростью велосипедист двигался дальше,если...
pedyxa12 pedyxa12  29.07.2019 17:00
(3,7- x)÷0,36=1,05 решите уравнение...
Rukisha03 Rukisha03  29.07.2019 17:00
Найдите градусные меры углов треугольника мнк,если м меньше угла н на 40градусов и больше угла к на 10 градусов....

Популярные вопросы