1. Математика
  2. Высшая. даны вершины треугольника

Высшая. даны вершины треугольника к, м, с. найти уравнения сторон треугольника; систему неравенств, определяющих треугольник; сделать чертеж. к(-6; 4), м( 3; -3), с(1; 2)

Оля030905 Оля030905    1   11.03.2019 07:40    1

Ответы
Jack1703 Jack1703  24.05.2020 21:02

Уравнение прямой по двум точкам записывается в виде

\frac{x-x_A}{x_B-x_a}=\frac{y-y_A}{y_B-y_A}

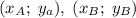где (x_A;\;y_a),\;(x_B;\;y_B) - координаты точек.

\frac{x-(-6)}{3-(-6)}=\frac{y-4}{-3-4}\\\frac{x+6}{9}=\frac{4-y}7\\7x+42=36-9y\\7x+9y+6=0\;-\;KM\\C(1;\;2)\Rightarrow7\cdot1+9\cdot2+6=7+18+6=310\Rightarrow7x+9y+6\geq0

\frac{x-3}{1-3}=\frac{y-(-3)}{2-(-3)}\\\frac{3-x}2=\frac{y+3}5\\15-5x=2y+6\\5x+2y-9=0\;-\;MC\\K(-6;\;4)\Rightarrow5\cdot(-6)+2\cdot4-9=-30+8-9=-31<0\Rightarrow5x+2y-9\leq0

\frac{x-1}{-6-1}=\frac{y-2}{4-2}\\\frac{1-x}7=\frac{y-2}2\\2-2x=7y-14\\2x+7y-16=0\;-\;KC\\M(3;\;-3)\Rightarrow2\cdot3+7\cdot(-3)-16=6-21-16=-31<0\Rightarrow2x+7y-16\leq0

Система неравенств, определяющих треугольник:

\begin{cases}7x+9y+6\geq0\\5x+2y-9\leq0\\2x+7y-16\leq0\end{cases}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
ltandreeva2016 ltandreeva2016  18.04.2020 18:55
Найти sinX=a,когда X€[-360°;360°] графику y=sinX и y=a...
anyanaffanya anyanaffanya  18.04.2020 18:55
[ ] всем привет, домашка по матеше, 6 класс. решаете, - получаете .​...
EvaSwansea12 EvaSwansea12  18.04.2020 18:54
Валерий поместил в банк вклад в размере 10 млн рублей на четыре года под 5% годовых. В начале третьего и четвёртого годов он дополнительно решил пополнять его на...
sanjabr82oymx7f sanjabr82oymx7f  18.04.2020 18:55
Вычислить косинус и у выражения на картинке...
madina319 madina319  18.04.2020 18:55
2^х + 2^-х = 2 сos 2xДо ть з лівою частиною З правою трохи легше...
ЮлічкаВдовіна ЮлічкаВдовіна  18.04.2020 18:55
X+2/4 + 4x-7/3 - 9-x/12 = 1...
ppqpl ppqpl  18.04.2020 18:55
Ширина прямоугольника в 3 раза меньше длинны найди площадь этого прямоугольника если его периметр равен 32 см...
alexlol228 alexlol228  18.04.2020 18:55
Вычтите дробь из смешанного числа ​...
Amaliya211013 Amaliya211013  18.04.2020 18:55
3+3+3+3+3+3+3+3+3+3+3+3+3+3+3+3+3+3+3+3=?...
9092005apv 9092005apv  18.04.2020 18:55
В треугольнике АВС угол С равен 121°. Найдите внешний угол при вершине С. ответ дайте в градусах...

Популярные вопросы