1. Математика
  2. Высота конуса равна 6. осевое

Высота конуса равна 6. осевое сечение- треугольник с углом 120 градусов. найдите площадь сечения, проходящего через две образующие, угол между которыми равен 30

nilovaekaterin nilovaekaterin    3   02.10.2019 03:10    0

Ответы
sanya3344 sanya3344  09.10.2020 10:53

Т.к. в осевом сечении образуется равнобедренный треугольник ASB с углом ASB = 120° и высотой SO = 6, то можем найти SA = SB = 12 (из прямоугольного треугольника ASO, в котором угол SAO = 30°).

Т.е. длина образующих конуса равна 12, а площадь треугольника образованного двумя образующими, между которыми угол в 30° равна:

S=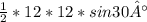\frac{1}{2} *12*12*sin30°=36

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
averianova1986 averianova1986  05.04.2020 06:55
с уравнением: 30336:х+537=921...
1AnastasiaP 1AnastasiaP  05.04.2020 06:56
Поставь вместо ∗ такое число, чтобы получилось верное равенство: 147,64=−∗....
tanyaaksenova1 tanyaaksenova1  05.04.2020 06:56
Найти соотношения квадратных чисел(-0,2)и(-0,4)...
КетиШифр КетиШифр  05.04.2020 06:56
Радиус окружности, задаваемой уравнением y=x^2-2x+y^2-6y-15=0. Равен...
MariyaMirnaya MariyaMirnaya  05.04.2020 06:56
В случае засухи вода понизится на 1 метр.Отметь новый уровень воды в колодце после засухи. -1м. | |___? м. - подпиши новый уровень воды | |-2 м....
Asel272727 Asel272727  05.04.2020 06:57
Очень вас Буду очень благодарна...
Dasha826251 Dasha826251  05.04.2020 06:57
Как называется число, которое делят?...
mamatvoeymamy mamatvoeymamy  05.04.2020 06:57
Один з коренів квадратного рівняння х²-7х+q=0 дорівнює 2. Знайдіть інший корінь рівняння та коефіцієнт q. 2.Складіть квадратне рівняння з цілими коефіцієнтами, якщо...
skybeast skybeast  05.04.2020 06:57
Часткa від дїлення двох чисел з різними знаками є число 2) Знайдить значення виразу ( 2m + 8m ) :5 якщо m= -12. Обчисліть значення виразу a : b. якщо a= -36. b= -6​...
1232957 1232957  05.04.2020 06:57
С об яснением Ето не сложно!...

Популярные вопросы