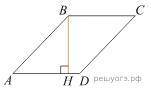
Высота BH ромба ABCD делит его сторону AD на отрезка AH=12 и HD=1. Найдите площадь ромба.

Привет! Давай разбираться с этой задачей.

У нас есть ромб ABCD, и нам нужно найти его площадь. Для этого нам понадобятся дополнительные знания о ромбах.

Первое, что нам известно - это то, что высота BH ромба делит его сторону AD на два отрезка: AH = 12 и HD = 1. Это означает, что отрезок AD можно разделить на три равных отрезка: AH, HB и BD.

Для начала, давай найдем значение стороны ромба. Сумма всех трех отрезков, на которые мы разделили сторону AD, должна быть равна ее длине. Значит, AH + HB + BD = AD.

Мы знаем, что AH = 12 и HD = 1, поэтому BD = AD - AH - HD. Подставим значения и получим BD = AD - 12 - 1. Но мы также знаем, что BD = HB. Так что можем записать: HB = AD - 13.

Теперь найдем площадь ромба. Площадь ромба равна произведению длин двух его сторон, разделенному на 2. Формула для площади ромба: Площадь = (AB * BH) / 2.

Но у нас нет прямых данных о длине стороны AB и высоте BH. Однако у ромба AB = BC = CD = DA. Так что это значит, что AB = AD.

Теперь можем записать нашу формулу для площади ромба как: Площадь = (AB * BH) / 2 = (AD * BH) / 2.

Используем тот факт, что HB = AD - 13. Подставим это значение в нашу формулу: Площадь = (AD * (AD - 13)) / 2.

Но у нас все еще нет значения для AD. Тут нам помогут знания о ромбах.

Заглянем внимательно на рисунок. Видишь, что у нас есть прямоугольный треугольник AHD? Это означает, что есть теорема Пифагора, которая говорит, что сумма квадратов катетов равна квадрату гипотенузы.

В нашем случае катет AH = 12, катет HD = 1, и гипотенуза AD. Мы знаем, что AD^2 = AH^2 + HD^2. Заменяя значения, получаем AD^2 = 12^2 + 1^2 = 144 + 1 = 145.

Возведем в квадрат обе стороны этого равенства: AD = sqrt(145). Мы получили, что длина стороны ромба AD равна корню из 145.

Теперь можем подставить это значение в нашу формулу для площади ромба: Площадь = (sqrt(145) * (sqrt(145)-13))/2.

После всех используем калькулятор, выведем значение площади ромба, и ответ готов!