Выполняется ли необходимое условие сходимости ряда: 1/2+3/4+5/8+7/16+...
2. Исследовать сходимость ряда, используя предельный признак сравнения (в прикрепленном файле уравнение под цифрой 2)
3. Найти интервал сходимости степенного ряда и исследовать сходимость на концах интервала (уравнение на картинке без нумерации)
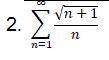
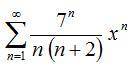
Другие вопросы по теме Математика
Популярные вопросы
- Найди значение выражения (-5,4 + 1,6 ) + ( -3,7 ) - ( -10,5 )...
3 - Краткий отзыв в.губарев королевство кривых зеркал...
1 - Найдите и отметьте приставки в словах: , истопник, полоска, поросенок,...
2 - 9^x-31*3^x+108≤0 решить уравнение....
2 - Вот полисахариды альдегидогруппы и кетогруппы не имеют, а дисахариды?...
1 - Влажность свежескошенной травы 60%, а сена 15%. сколько сена получится...
3 - Пристани a и b расположены на озере, расстояние между ними равно...
1 - Некоторая компания продаёт свою продукцию по цене p = 500 руб....
3 - Главные герои сказки принцесса на горошине...
2 - Найдите значение выражения 14(m6)5+11(m10)3/(5m15)2...
3
1. Необходимое условие сходимости ряда
Для начала, давайте посмотрим на данную последовательность: 1/2, 3/4, 5/8, 7/16 и так далее. Мы видим, что каждое следующее число в данной последовательности больше предыдущего числа, то есть каждый следующий член ряда больше предыдущего. Также, мы можем заметить, что каждое следующее число в данной последовательности стремится к 1.
Мы можем предложить такое предположение: последовательность сходится к 1. Чтобы проверить это предположение, мы можем использовать предельный признак.
2. Исследование сходимости с использованием предельного признака сравнения
Для применения предельного признака сходимости, мы должны найти соответствующий сходящийся ряд, сравнение которого даст нам ответ на вопрос о сходимости нашего данного ряда.
Давайте рассмотрим ряд 1/2 + 1/4 + 1/8 + 1/16 + ... (это геометрическая прогрессия с первым членом 1/2 и знаменателем 1/2). Этот ряд является сходящимся геометрическим рядом, так как абсолютная величина знаменателя (1/2) меньше 1.
Мы заметили, что каждый член нашего данного ряда больше соответствующего члена ряда 1/2 + 1/4 + 1/8 + 1/16 + ... Таким образом, мы можем утверждать, что сходимость нашего ряда будет слабее, чем сходимость ряда 1/2 + 1/4 + 1/8 + 1/16 + ...
Итак, так как ряд 1/2 + 1/4 + 1/8 + 1/16 + ... сходится, наш ряд также будет сходиться.
3. Нахождение интервала сходимости степенного ряда и исследование сходимости на его концах
Теперь давайте перейдем к нахождению интервала сходимости степенного ряда и исследованию его сходимости на концах интервала, используя уравнение на картинке.
На картинке есть два уравнения, но нас интересует только уравнение y = -0.5x + 1. Давайте решим это уравнение для x:
0.5x = 1 - y,
x = (1 - y) / 0.5.
Так как x является переменной в степенном ряде, у нас должно быть |x - a| < R, где a - центр интервала и R - радиус сходимости.
Исходя из уравнения на картинке, мы видим, что центр интервала равен 1 и R = 1 - a = 1 - (-1) = 2.
Таким образом, интервал сходимости степенного ряда будет (-1, 3). Теперь мы можем исследовать сходимость ряда на его концах, то есть когда x = -1 и x = 3.
Когда x = -1, мы получим ряд 1/2 - 3/4 + 5/8 - 7/16 + ..., где знаки членов ряда чередуются. Это альтернативный знак гармонического ряда, который сходится.
Когда x = 3, мы получим ряд 1/2 + 3/4 + 5/8 + 7/16 + ..., где знаки членов ряда все положительные. Этот ряд - положительный гармонический ряд, который расходится.
Итак, наш степенной ряд сходится в интервале (-1, 3), но расходится на его концах -1 и 3.
Надеюсь, мой ответ был понятен и полезен для вас. Если у вас возникнут еще вопросы, не стесняйтесь задавать их!