Выполнить преобразования и привести функция к виду y=ax^2 + bx + c
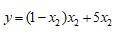
Другие вопросы по теме Математика
Популярные вопросы
- Инасекомых рой кусает защищая свои права на жизнь разъяснить эту цитату...
1 - Переведите стихотворение ільяса жансүгірова-күйші: қамаудың хан ауылы...
1 - Мэтынын турын аныкта 1.сипатау мэтены 2.энгымелеу мэтены 3.паымдау мэтены...
2 - 1.самая плодородная почва2.один из компонентов почвы3.разрушение почвы...
2 - Чому в україні відбувся демографічний вибух 1550р.? ...
2 - Доклад на тему: примеры противоохранности стран мира много ! надо на...
1 - Написать на ответы на вопросы.do you like sewing? 2 do you like reading?...
1 - Характеристика главных героев оперы иван сусанин...
2 - В200 г раствора азотной кислоты добавили 11,2 г найти массовую долю...
3 - Дописать пропущенные слова: закодированное сообщение можно декодировать...
2
Данная функция представлена в виде 3 скобок, где каждая скобка содержит три члена.
Начнем с первой скобки (-2x + 3). Внутри данной скобки есть два члена -2x и 3. Мы можем раскрыть эту скобку, записав произведение каждого члена в скобке на коэффициент a.
(-2x + 3) = -2ax + 3a
Теперь перейдем ко второй скобке (4x - 5). Внутри данной скобки есть два члена 4x и -5. Мы можем раскрыть эту скобку, записав произведение каждого члена в скобке на коэффициент b.
(4x - 5) = 4bx - 5b
Наконец, перейдем к третьей скобке (x + 2). Внутри данной скобки есть два члена x и 2. Мы можем раскрыть эту скобку, записав произведение каждого члена в скобке на коэффициент c.
(x + 2) = cx + 2c
Теперь соединим все полученные выражения:
-2ax + 3a + 4bx - 5b + cx + 2c
Теперь приведем подобные члены. В данном случае, мы можем объединить все члены с переменной x:
-2ax + 4bx + cx + 3a - 5b + 2c
Сгруппируем коэффициенты при каждой переменной:
(4b + c)x - 2ax + 3a - 5b + 2c
Теперь расположим члены в порядке убывания степеней переменной x:
-2ax + (4b + c)x + 3a - 5b + 2c
Таким образом, приведенная функция имеет вид y=ax^2 + bx + c, где коэффициент при x^2 равен 0 (так как нет члена с переменной x^2), коэффициент при x равен 4b + c, коэффициент при константе равен 3a - 5b + 2c.
Итак, в ответе получаем:
y = -2ax + (4b + c)x + 3a - 5b + 2c