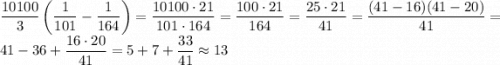Вычислите значение выражения 10100(1/101*104+1/104*107+...+1/161*164) и округлите его до единиц.
Другие вопросы по теме Математика
Популярные вопросы
- Прочитайте фрагмент словаря русских синонимов Обратите внимание на чистоту употребления...
1 - надо выбрать ОДИН ЛЮБОЙ пункт...
1 - В чем суть растрового подхода к представлению графической информации...
1 - Решить уравнения: 1,6(8x+10)= -6,4...
3 - Прочитайте текст, выпишите ключевые слова (5-7), определите главную мысль слова:...
3 - с литературой 1. Кто из витязей отправляется на поиски Людмилы? 2. Кто ожидает...
3 - Определите спряжение глаголов по неопределенной форме. Образуйте от каждого глагола...
1 - ТРЕНАЖЕР ПО МАТЕМАТИКЕ НА ТЕМУ «ПРОЦЕНТЫ» 1. Перевести десятичную дробь в проценты:...
3 - х-2/9=5/12х+1 1/3 2) 2/3(4 1/2х-3/5)-5/7(7/15х-7/9)=-1 32/45...
1 - СОСТАВИТЬ ФОРМУЛЫ ИЗОМЕРОВ ДЛЯ ВЕЩЕСТВА ТОЛЬКО ПРАВИЛЬНО, ВЫБЕРУ ЛУЧШИМ ОТВЕТ....
1
Заметим, что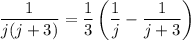 . Поэтому
. Поэтому 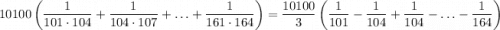 то есть
то есть