Вычислите значение производной функции
y=(4x+6)^4(x-3) в точке х=-1,5

Ответы

CwetochekAnfisa 17.08.2022 07:19

значение производной функции

y=((4x+6)^4)*(x-3) в точке х=-1,5 равно 0

Пошаговое объяснение:

Рассмотрим два случая

В первом условие задачи выглядит так

$y = (4x+6)^4 \cdot (x-3) ~~ ; ~~ x _0 = -1,5$

Во втором

$y = (4x+6)^{4(x-3)} ~ ; ~ x_0 = - 1,5$

В первом случае

$y = (4x+6)^4 \cdot (x-3) ~~ ; ~~ x _0 = -1,5$

Вспомним что :

$\bullet ~ ~(u \cdot v )' = u'v + uv' \bullet ~~ f(g(x)) = f'(g(x))\cdot g'(x)$

Находим производную :

$y ' = ((4x+6)^4 \cdot (x-3)) = ((4x+6)^4)'\cdot (x-3) + (4x+6)^4\cdot (x-3)' y '= (4x+6)'\cdot 4(4x+6)^3\cdot (x-3) + (4x+6)^4 y ' = (x-3)\cdot 8x\cdot (4x+6)^3 + (4x+6)^4 y' = (4x+6)^3 (8x^2 -24x )+(4x+6)^4$

Теперь находим производную в точке x = -1,5

$y'(-1,5) =\underbrace{\Big (4 \cdot (-1,5) + 6 \Big) }_0 \cdot \Big (8 (-1,5)^2 - 24\cdot1,5 \Big)+\underbrace{\Big (4 \cdot (-1,5) + 6 \Big)^4 }_0 = 0$

Во втором случае

$y = (4x+6)^{4(x-3)} ~ ; ~ x_0 = - 1,5$

$y = (4x+6)^{4(x-3)} = \left (e^{\ln(4x+6)} \right)^{4x-12} = e^{\ln (4x+6)\cdot (4x-12)}$

Теперь находим производную используя правила :

$\bullet ~~ (e^{u} ' ) = u ' \cdot e^{u} \bullet ~ ~(u \cdot v )' = u'v + uv' \bullet ~(\ln x ) ' = \dfrac{1}{x}$

$y '= \left (e^{\ln (4x+6)\cdot(4x-12)}\right)' = e^{\ln (4x+6 )\cdot (4x-12)}\right \cdot \Big(\ln(4x+6) \cdot (4x-12)\Big)' y ' = (4x+6)^{4x-12}\cdot \bigg(\dfrac{1}{4x+6}\cdot (4x-12)+ 4\ln(4x+6) \bigg )$

При подстановке x = -1,5

Знаменатель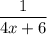 $\dfrac{1}{4x+6}$ равен нулю , а значит условие в данном случае некорректное , и условие должно быть как в первом случае , и ответ на задачу 0