вычислите угол ВАС треугольника АВС с вершинами А(2;0) В(5;0) С(5, корень 3)
Другие вопросы по теме Математика
Популярные вопросы
- ато мама убьёт кто первый ответит тому лучший ответ и подписка....
3 - 1. Вычислите массу воздуха в кабинете с объемом 120 м3 при давлении...
3 - Заполните пропуск: That s the stadium ... we played football last summer.1)...
2 - Құрылғыларынсыз по составу...
2 - Сочинение на тему: Уважение к черта , отличающая цивилизованность от...
3 - Упрощение $16\cdot \frac{1}{4}$плюс обратная $- \frac{1}{2}$сторона...
2 - Выполните задание по английскому языку...
2 - Put the verbs in brackets into the correct from.where... Roger ... (to...
2 - Как распространяется семена подсолнуха...
2 - Запитання й завдання 1. Чому народи Африки до початку великих географічних...
2
угол ВАС=30*
Пошаговое объяснение:
Вершинами А(2;0) В(5;0) С(5,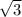 )
)
угол BAC-> cosa=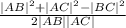
обычная формула для нахождения косинуса угла
Теперь
AB=((5-2);(0-0))=(3;0)
AC=((5-2);(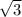 -0))=(3;
-0))=(3;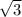 )
)
BC=((5-5);(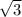 -0))=(0;
-0))=(0;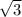 )
)
из
Теперь |AB|=
То есть |AB|=3
|AC|=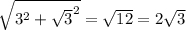
|BC|=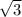
cosa=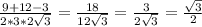
a=arccos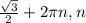 ∈ Z
∈ Z
a=30+2πn, n ∈ Z
30 градусов