1. Математика
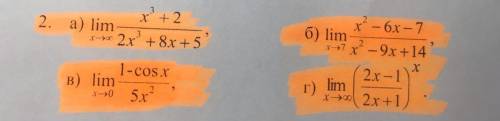
  2. Вычислите пределы под а)б)в)г)

Вычислите пределы под а)б)в)г)


Вычислите пределы под а)б)в)г)

кек945 кек945    1   25.01.2021 22:18    0

Ответы
TheRidGames TheRidGames  24.02.2021 22:25

Пошаговое объяснение:

а)

\displaystyle \lim_{x \to \infty} \frac{x^3+2}{2x^3+8x+5} = \lim_{x \to \infty} \frac{1+\frac{2}{x^3} }{2+\frac{8}{x^2} +\frac{5}{x^3} } =\frac{1}{2}

б)

\displaystyle \lim_{x \to 7} \frac{x^2- 6x-7}{x^2-9x+ 14}

так как числитель и знаменатель обращаются в нуль при x=7, то 7 – корень обоих многочленов, а значит, каждый из них разлагается на множители, одним из которых будет (x - 7) .

x² -6x -7 = (x-7)(x+1)

x² - 9x +14 = (x-7)(x-2)

и тогда получим

\displaystyle \lim_{x \to 7} \frac{x^2- 6x-7}{x^2-9x+ 14}= \lim_{x \to 7} \frac{(x-7)(x+1)}{(x-7)(x-2)} = \lim_{x \to 7} \frac{x+1}{x-2 } = \frac{8}{5}

в)

\displaystyle \lim_{x \to 0} \frac{1-cosx}{5x^2}

1-cos = 2sin²(x/2)

следствию свойства первого замечательного предела

sinx ≈ x, тогда 2sin²(x/2) ≈x²/2

и вот что получилось

\displaystyle \lim_{x \to 0} \frac{1-cosx}{5x^2}= \lim_{x \to 0} \frac{2sin^2(x/2)}{5x^2} = \lim_{x \to 0} \frac{\frac{x^2}{2} }{5x^2} =\frac{1}{10}

г)

здесь применим свойство второго замечательного предела

\displaystyle \lim_{x \to \infty}(1+\frac{a}{x} )^{bx}=e^{ab}

\displaystyle \lim_{x \to \infty} (\frac{2x-1}{2x+1} ) ^X= \lim_{x \to \infty}(1+\frac{-2}{2x+1} )^\displaystyle{\frac{2x}{2} }}= \lim_{x \to \infty} (1+\frac{-2}{2x+1} )^ \displaystyle {\frac{1}{2} (2x+1)} }=

\displaystyle =e^\displaystyle{(-2)*\frac{1}{2} }= e^{-1} =\sqrt{e}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Анц Анц  04.01.2021 10:39
Дуги AM, MB, AB являются половиной окружностиA-B ВM​...
Litoli Litoli  04.01.2021 10:43
3. Дан четырехугольник, как показано на рисунке: 5CM22а) ( ) Найдите сумму длин известных сторонфигуры.BС213 смb) ( ) Периметр фигуры2222Найдите длину стороны CD.A7...
nastyamashkina12 nastyamashkina12  04.01.2021 10:44
Сколько процентов квадрата закрашено?​...
irinaira72rt irinaira72rt  04.01.2021 10:45
Какую из данных дробей нельзя представить в виде конечной десятичной дроби? a) b) 25 4a+2b=9 [1] [2] 2. Выразите переменную b через переменную а в выражении 3. Раскройте...
СвинкаГоппа СвинкаГоппа  04.01.2021 10:46
87. Через прямую и точку, не лежащую на этой прямой… A) они пересекаются по прямой, проходящей через данную точку B) все точки этой прямой лежат на данной плоскости...
ahmetoadilnaz1 ahmetoadilnaz1  04.01.2021 10:51
В магазине продаются бакалейные товары в упаковках. На рисунке показаны цены. Гречневая крупа 75 руб. гречка.png Перловая крупа 40 руб. перловка.png Пшеничная крупа...
RokkuKun RokkuKun  04.01.2021 10:51
Учитель дал одному ученику 2 ореха, а всем остальным по 5. Если бы он всем дал по 4 ореха, то у него осталось бы 15 орехов. Если общее число ореховучителя равно х,...
adamannik adamannik  04.01.2021 10:53
Составьте одну из возможных формул n-го члена последовательности по первым пяти ее членам: 1/2 ; 2/3 ; 3/4 ; 4/5 ; 5/6 ​...
kolya144 kolya144  04.01.2021 10:56
5. Решите уравнение 53x = 25х+1,5А) -1 B) 1 C) 4D) 3​...
shvbur75 shvbur75  04.01.2021 11:07
Сколько есть ДВУЗНАЧНЫХ чисел кратных к 15 но не кратных 9​...

Популярные вопросы