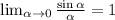Вычислите предел: sin10x/5x lim x-->0
Другие вопросы по теме Математика
Популярные вопросы
- Материальная точка колеблется с частотой 10 гц. укажите период колебаний и число...
2 - На 4 одинаковых платья пошло 16 м.ситца.сколько таких платьев получится из 20м.ситца?...
1 - Выбери приметы, характерные для осени (найди и укажи правильный полный ответ) а)...
3 - Подбери подходящие по смыслу слова и запишите словосочетания догонишь,осмотрит,...
2 - Выпишите отдельно слова неоднородные! - ну, уже успел всё изложить! - послышался...
1 - Укажите названия государств, участвовавших вместе с германией в агрессии против...
2 - Найти закономерность слов коньки, лес, обруч, слова для справок плавание,гимнаст,...
1 - Две параллельные прямые пересечены секущей. один из восьми образовавшихся углов...
3 - Масса каждого новаражденных телят была следуещей 9 кг 800 г 12 кг 700 г 11 кг 500...
2 - Самая высокая (низкая) точка поверхности западно сибирской равнины, ее название...
1
Пошаговое объяснение:
Неопределённость 0/0. ⇒
Берём производную одновременно от числителя и знаменателя:
ответ: 2
===================
Пошаговое объяснение: используется первый замечательный предел: