Вычислите предел последовательности
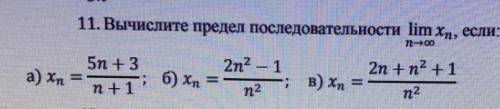
Другие вопросы по теме Математика
Популярные вопросы
- Записать с логико- символов и построить отрицание: для любого натурального...
1 - Пусть м — точка пересечения медиан остроугольного треугольника авс....
3 - Choose a/an or no article . 1. when i was , i used to be very shy....
2 - 9класс социально- развитие страны в первой четверти xix века....
3 - Перпендикуляром, проведённым из точки j к прямой as, является: sb...
1 - Вычислите количество теплоты переданное спирту массой 1 кг для превращения...
1 - Напишите сказку на тему «кипение»...
1 - Азақ тілі мәтінді жалғастыру 93 бет 1 тапсырма көмектесіндерші өтінем...
2 - Адская бездна, первая глава песнь среди раскатов грома . краткое...
3 - Кого парижские бедняки называли другом народа? ...
1
Есть замечательное правило, разобрав которое Вы больше никогда не будете обращаться за в подобных примерах. Итак, если х стремится к ∞, а в числителе и знаменателе многочлены стандартного вида, т.е. такие, которые уже не упрощаются. то смотрим на показатели высших степеней числителя и знаменателя. Если показатель числителя больше показателя знаменателя, ответ ∞, если меньше, то ответ ноль, а если равны, то делите коэффициент числителя на коэффициент знаменателя.
Разберем Ваш пример. а) Числитель 5n+3 - стандартный вид многочлена, показатель степени старшего члена 5n=5n¹ равен 1. Знаменатель n+1 - стандартный вид многочлена, показатель степени старшего члена n=n¹ равен 1. показатель числителя равен показателю знаменателя⇒ коэффициент числителя 5n равен 5, коэффициент знаменателя n=1n равен 1, делим коэффициент числителя на коэффициент знаменателя.5/1=5.
б) аналогично 2/1=2
в) 1/1=1
В б) и в) у старших членов многочленов степень вторая, а коэффициенты соответственно 2 и 1; и 1 и 1.