Вычислите предел функции limx→0 √2+x-√2-x/5x 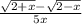
Другие вопросы по теме Математика
Популярные вопросы
- Придумай и запиши предложения с однородными членами дополнительные слова ручка тетрадь...
2 - Обчисліть объем правильної чотирикутноіі призми, сторона основы якоіі дорівнює 6...
1 - Напишите небольшое сочинение на тему «Самое яркое впечат-ление моего детства»....
2 - Скласти речення за схемою [ ] , (що) , (тому що) , і [ ] ....
3 - Які цифри можна підставити замістьзірочки, щоб округлення буловиконано правильно...
3 - Найди относительную молекулярную массу цинксодержащего вещества X:ZnO−→−−−−+HNO2А−→−−−−−−−+H2SO4(к),tБ−→−−+MgВ−→−−+S,tX.ответ:...
1 - ОООЧЕНЬ У прямокутному трикутнику гiпотенуза дiлиться точкою дотику вписаного кола...
1 - Викторина по сказке Х.К. Андерсена «Соловей». 1. Кому в сказке Х.К. Андерсена «Соловей»...
1 - І частина. Вікторина на краще знання героїв повісті. 1. «В її устах і душі насіння...
3 - Дано коло з центром О. Визнаєте градусну міру ДІАМЕТР АВ утворено з ходою ВС кут...
3
Пошаговое объяснение:
домножаем числитель и знаменатель на выражение, сопряженное числителю