Вычислите площади фигур, заданных указанными линиями. 1) x-y+3=0, x+y-1=0, y=0 2.) y=x^2+1, y=0, x=-1, x=2 пункт 1 в 13 и 15.
Другие вопросы по теме Математика
Популярные вопросы
- Write a short review of film that you like. напишите про бриллиантовую руку....
3 - Получите спирты из соответсвующих галоленпроизводных: -бутанол -2 -пропандиол...
3 - Опишите портрет какой то женщины. (картина). используйте краски, прилагательные,...
2 - Визначити довжину маятника,який коливається з частотою 5 гц в умовах землі....
3 - Просклонять слово чувства 3 склонением !...
3 - Спільнокореневі до слів: підвода, річний, будити, листок...
1 - Составить предложение с словосочетанием уйти прочь или отворить настежь =)...
1 - Какие вещества тспользуются в быту и где...
1 - Представьте выражение в виде дроби 5y-(2-4y^2)/3y...
3 - Напишите сочинение в художествнном стиле на тему музыка(желательно рок)...
1
ответ Замятина - сначала думаем:
1. Фигура ограничивается двумя функциями по высоте - по оси ординат (ось ОУ) и двумя точками по ширине - по оси абсцисс (ОХ).
2. Площадь это интеграл разности функций в пределах интегрирования - по оси ОХ.
3. Пределы интегрирования или заданы или находятся как точки пересечения функций.
4. Важно знать какая функция на графиках выше, чтобы составить правильную разность.
5. Рисунок к задаче позволяет упростить процесс решения.
ДАНО: х-у+3=0, х+у-1=0, у=0.
НАЙТИ: S=? - площадь фигуры.
РЕШЕНИЕ.
Даны уравнения прямых. Приведем их к каноническому виду.
1) у1 = х+3 и у2 = -х + 1. у3 = 0.
Делаем рисунок - рисунок в приложении. Видим, что фигура - это два прямоугольных треугольников и координата точки пересечения А(-1;2), а две других вершины в точках: В(-3;0) и С(1;0). Глаза видят, а руки пишут формулы: находим пределы интегрирования.
2) y1 = y3 =x+3= 0, a = -3 - нижний предел интегрирования - начало.
3) y1 = y2, x+3 = - x + 1, 2*x = - 2, b = -1 - общий предел.
4) y2 = y3, -x+1 = 0, c = 1 - верхний предел интегрирования.
Переходим к интегрированию. Для удобства найдем площади треугольников отдельно.
5)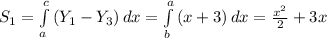
6) Вычисляем - верхний предел - b = -1 , нижний - а = -3
S1(-1) = 1/2 -3 = - 2.5, S1(-3) = 4.5 -9 = - 4.5,
S1 = -2.5 - (-4.5) = 2 - площадь левого (красного) треугольника.
Интегрируем разность функций на втором участке - от -1 до 1.
7)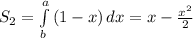
Вычисляем интегралы на границах.
S2((-1) = 1.5, S2(1) = -0.5,
S2 = 1.5 - (-0.5) = 2.
И окончательно - сумма интегралов.
S = S1 + S2 = 2+2 = 4 (ед.²) - площадь - ответ.
Можно проверить - половина площади прямоугольника - 4*2 = 8.
Правильно.
2) ДАНО: Y1= x²+1, Y2 = 0, b = - 1, a = 2.
Делаем рисунок - в приложении. Здесь фигура описана одной функцией. Сразу переходим к интегрированию. Внимание! Предлагается писать функцию по возрастанию степени при Х.
1)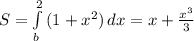
Вычисляем на границах интегрирования.
S(2) = 2 + 2 2/3 = 4 2/3 (4,667) , S(-1) = -1 - 1/3 = - 1 1 /3 (-1,333)
S = 4 2/3 - (- 1 1/3) = 6 (ед.²) - площадь - ответ.
ответ Замятина - расчет проверен, а в записи могут быть и опечатки - я не виноват.