1. Математика
  2. Вычислите площадь фигуры

Вычислите площадь фигуры ограниченной линиями y=9-x в квадрате и y=5

NuznaPomojs NuznaPomojs    3   22.03.2019 11:02    1

Ответы
у2цциволв1 у2цциволв1  26.05.2020 15:16

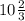
S=10\frac{2}{3}

Пошаговое объяснение:

Для определения пределов интегрирования находим координаты пересечения графиков по оси х

-х²+9=5

-х²=-4

х1=2

х2=-2

\int\limits^2_{-2} {9-x^2} \, dx =9x-\frac{1}{3} x^3 |_{-2} ^2=(9*2-\frac{8}{3} )-(9*(-2)+\frac{8}{3} )=15\frac{1}{3} -(-15\frac{1}{3} )=30\frac{2}{3}

\int\limits^2_{-2} {5} \, dx =5x|_{-2} ^2=5*2-5*(-2)=20

30\frac{2}{3} -20=10\frac{2}{3}

График в файле.


Вычислите площадь фигуры ограниченной линиями y=9-x в квадрате и y=5
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
eldos4 eldos4  11.08.2019 08:00
Теплоход проходит 40 целых одну вторую километра по течению реки за одну целую одну вторую часа на сколько больше времени уйдет на обратный путь если скорость течения равна 3 целых...
КириллFace КириллFace  11.08.2019 08:00
Придумайте на нахождение двух чисел по их сумме и разности. чтоб числовые данные для подобраны были хорошо и она имела решение. прочитать в классе, чтоб она имела решение...
ivan504 ivan504  11.08.2019 08:00
Сделать презентацию на тему банан в шоколаде посыпанный кокосовой стружкой что должно быть 1. создания. 2.отличие 3.об стране 4.особенности кухни 5.интересные моменты....
ЖеняРай ЖеняРай  11.08.2019 08:00
Периметр треугольникаbmp равен 128 мм. известно, что сторона bm равна 5 см 6 мм, а сторона mp в два раза короче bm. определите длину стороны bp....
Bisspector Bisspector  11.08.2019 08:00
Как составить краткую запись на каждом этаже 11этажного дома по 3 квартиры каждая квартира в доме 3 комнатная сколько комнат во всем доме...
FuNTowNToPPlay4ik FuNTowNToPPlay4ik  11.08.2019 08:00
Протяжённость маршрута для гонок 300 км на этом маршруте 3 этапа длина 1 и 3 этапа вместе 180 км а 2 и 1 200 км найди длину 3 этапа...
Оля010720 Оля010720  11.08.2019 08:00
Решите уравнение (8 2/5: x+3 5/9): 4 1/6=1 1/3...
alena5378 alena5378  11.08.2019 08:00
Как решить уравнение 117-(12-x)=109...
smirnovigor smirnovigor  11.08.2019 08:00
Длина прямоугольника на 13 метров больше чем его ширина площадь прямоугольника равна 140 квадратных сантиметра найдите пример периметр прямоугольника...
ibrohim0775 ibrohim0775  11.08.2019 08:00
Повідомлeння чому я люблю свою маму...

Популярные вопросы