1. Математика
  2. Вычислите площадь фигуры,

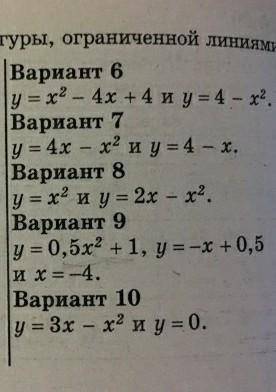
Вычислите площадь фигуры, ограниченной линиями: только 9 Вариант
​


Вычислите площадь фигуры, ограниченной линиями: только 9 Вариант ​

valerea0 valerea0    2   20.10.2020 07:02    0

Ответы
влад2318 влад2318  19.11.2020 07:03

Условие:

Вычислить площадь фигуры, ограниченной линиями:

y=0,5\cdot x^2+1;\\y=-x+0,5;\\x=-4;

Такая фигура называется криволинейной трапецией, а ее площадь находится по следующей формуле:

S=\int\limits^b_a {[y_1(x)-y_2(x)]} \, dx

Ограничивающие функции y₁(x) и y₂(x), а также левая граница интервала a = -4 нам известны по условию задачи. Чтобы найти правую границу b приравняем функции y₁(x) и y₂(x) и решим уравнение.

0,5\cdot x^2+1=-x+0,5;\\0,5\cdot x^2+x+0,5=0;|\cdot 2\\x^2+2x+1=0\\\\D=2^2-4=0\\\\x_{1,2}=\frac{-2 \pm 0}{2}=-1

Таким образом правая граница b = -1 найдена.

Найдем интеграл

S=\int\limits^{-1}_{-4} {[0,5\cdot x^2+1-(-x+0,5)]} \, dx=\int\limits^{-1}_{-4} {[0,5\cdot x^2+x+0,5)]} \, dx=\\\\=(\frac{x^3}{6}+\frac{x^2}{2}+0.5x )\bigg|^{-1}_{-4}=\frac{1}{6}\cdot (-1-(-64))+ \frac{1}{2}\cdot (1-16) +0,5\cdot (-1-(-4))=\\\\=\frac{63}{6} -\frac{15}{2}+\frac{3}{2} =\frac{21}{2} -\frac{12}{2}=\frac{9}{2} =4,5

ответ: S = 4,5

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
yliana23 yliana23  08.04.2020 09:47
Как найти среднюю скорость движения? только нужно коротко...
katysca katysca  08.04.2020 09:47
Каким будет решение? Пример:(х + 10) · 2 = 20ответ я знаю. X = 0. Но вот как записать само решение я не понимаю....
СоняКот2000 СоняКот2000  08.04.2020 09:47
Жил-был Джеки-Джек — щенок и отважный боец, и было у него 7 сушек. Однажды утром Джеки-Джек съел 2 сушки. Потом подумал-подумал, дождался обеда и съел ещё 4. Сколько...
protekte protekte  08.04.2020 09:47
Желательно максимально понятно даю ​...
del9832 del9832  08.04.2020 09:47
В кино пошли 23%, а на футбол - четверть всех учащихся класса. Куда пошло больше учащихся этого класса - в кино или на футбол? 1)на футбол 2)в кино и на футбол пошло...
Lalalila03denchik Lalalila03denchik  08.04.2020 09:47
Представьте в виде многочлена выражение 1) (-5-2а)² 2) (2¼а+1 ⅔b)² 3) ( 6pq²-qp²)² 4) (2x⁴+5x³b(степень 5))...
ArtemikLis ArtemikLis  08.04.2020 09:47
Найти первообразную для функции f(x) = 1/(7-3*x)^5...
olesjaozs5is olesjaozs5is  08.04.2020 09:47
Знайдіть корені рівняння 2х²+х-1=0. (HELP)...
Lop1234kop Lop1234kop  19.09.2019 19:51
Найдите площадь поверхности стола если длина составляет 150 см, а ширина 50 см​...
Ооооооокккккккк Ооооооокккккккк  19.09.2019 19:51
Расся циррои о.(82) которые из решений неравенства кратны 9: 1) 453 x 500; 2) 35 у 70; 3) 44 x 72? o​...

Популярные вопросы