1. Математика
  2. Вычислите площадь фигуры

Вычислите площадь фигуры ограниченной линиями : 1) y=x^2, 2) y= x+2

ponomarevdenisow2kh1 ponomarevdenisow2kh1    1   29.09.2019 18:10    0

Ответы
3Человек3 3Человек3  11.08.2020 09:21
Найти площадь фигуры, ограниченной кривыми.

Для решения задачи в первую очередь нужно построить график.

По графику видно, что найти нам нужно площадь области, лежащей над параболой y = x² и под прямой y = x + 2.

Найдём точки пересечения данных кривых. Для этого нужно решить систему из уравнений их функций.

\begin{cases}y = x^2,\\y = x + 2;\end{cases}\\\\x^2 = x + 2;\\x^2 - x - 2 = 0;\\D = [b^2 - 4ac] = (-1)^2 - 4\times(-2) = 1 + 8 = 9 = 3^2;\\x_{1,2} = \left[\dfrac{-b\pm\sqrt{D}}{2a}\right] = \dfrac{1\pm 3}{2};\\x_1 = 2, x_2 = -1.

Найти площадь фигуры, ограниченной сверху графиком функции y = x + 2, а снизу функцией y = x², а так же прямыми x = 2 и x = -1, значит вычислить следующий определённый интеграл.

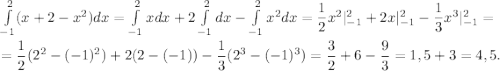
\int\limits^{2}_{-1}(x + 2 - x^2) dx = \int\limits^{2}_{-1}x dx + 2\int\limits^{2}_{-1}dx - \int\limits^{2}_{-1}x^2 dx = \dfrac{1}{2}x^2|^{2}_{-1} + 2x|^{2}_{-1} - \dfrac{1}{3}x^3|^{2}_{-1} =\\\\=\dfrac{1}{2}(2^2 - (-1)^2) + 2(2 - (-1)) - \dfrac{1}{3}(2^3 - (-1)^3) = \dfrac{3}{2} + 6 - \dfrac{9}{3} =1,5 + 3 = 4,5.

ответ: 4,5.
Вычислите площадь фигуры ограниченной линиями : 1) y=x^2, 2) y= x+2
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
ура6 ура6  05.06.2019 03:00
Расшифруй записи( одинаковыми буквами обозначены одинаковые цифры,а разными - разные) а а с д 2 м + а 2 - 2 д с м к б а б 5 д 4 + м к н к м к...
tyupina2018 tyupina2018  05.06.2019 03:00
9,99 сколько это в процентах? 9 сколько в процентах?...
liqwer liqwer  05.06.2019 03:00
Между какими натуральными числами расположено число 4,02...
manoco manoco  05.06.2019 03:00
Решить : длиной 5м весит 175кг . сколько весит такая же длиной 7м...
12355689 12355689  05.06.2019 03:00
Надо составить слово из букв жандер....
aidarbI4123 aidarbI4123  05.06.2019 03:00
Напишите ответы. 256: 10, 37,5: 10, 3: 100, 70,2: 100...
Stultus Stultus  05.06.2019 03:00
Решить гонец должен был доставить депешу из афин в олимпию . 4 часа он мчался на лошади со скоростью 36/км.ч. а остальной путь вынуждин был бежать со скоростью 8/км.ч. в котором...
SkipMe SkipMe  05.06.2019 03:00
Решите уровнение 3 целых 11/24-x=1целая 1/6+1целую 1/9 за ранее блогадарен...
мопс22 мопс22  05.06.2019 03:00
Прочитай следующие числа и выпиши в столбик четные,во второй столбик не четные.третий столбик трехзначные,четвертый круглые числа 311 900 587 21 110 60 600 204 630 98 406...
ULYA1111111 ULYA1111111  05.06.2019 03:00
Умальчика в коллекции было 24 болгарских марок и 40 марок. он поместил их в альбом,поровну на каждую страницу. марки заняли на 2 страницы больше,чем болгарские. сколько страниц...

Популярные вопросы