Вычислите определенный интеграл
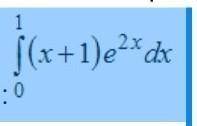
Другие вопросы по теме Математика
Популярные вопросы
- Определите события, которые характеризуют буржуазно- демократические...
2 - Прочитайте роман «Капитанская дочка». Запишите результаты своих...
3 - Користуючись методом електронного балансу доберіть коефіцієнти...
3 - Які три із зазначених понять та термінів доречні в описі зображеної...
2 - Визначити положення у періодичній системі хімічних елементів обчисліть...
3 - Засчитывается ли очко забитый головой баскетбол...
2 - Какие интересные игры есть на андроид? Онлайн или оффлайн без разницы...
3 - Почему дворцовые перевороты можно считать дворянскими? Почему вокруг...
2 - Речення зі словом глибинний...
3 - Составьте в тетради план по темен...
2
Вычислим неопределенный интеграл:
1)
2)
Итого:
Вычислим пределы интегрирования:
ответ: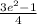 кв. ед.
кв. ед.