, ВЫЧИСЛИТЕ ОПРЕДЕЛЁННЫЕ ИНТЕГРАЛЫ
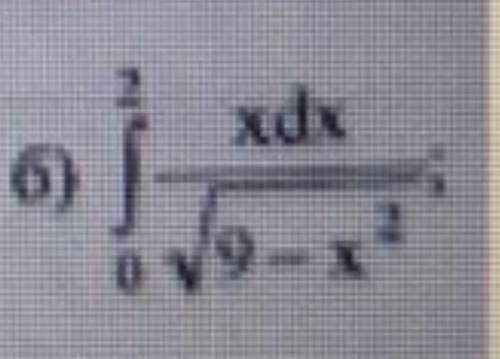

Другие вопросы по теме Математика
Популярные вопросы
- 3.Від краплі олії, що має заряд +q, відокремили крапельку з зарядом...
3 - 7класс по химии. напищите (можете сфотографировать ответ структурные...
3 - Запишіть елементи сюжету повісті Лесі Ворониної Таємне товариство...
2 - У нашім краї, на землі, нічого кращого немає, як тая мати молодая...
1 - Найти десять белорусских авторов и их произведения про маму...
2 - Практична робота №4 історія України Сорочинська ОЧЕНЬ ПОСТАВЛЮ МАКСИМАЛЬНИЕ...
2 - Переменные расходы семьи включают затраты: а) на еду, коммунальные...
3 - ответьте на вопросы The History of Computer Development The rapidly...
2 - 3. AMISTAKE DETECTORFind vocabulary mistakes.This book is interested....
1 - ЛИТЕРАТУРА 7 класс Очень ! В каких ситуациях общения нужно использовать...
2
По частям: