Вычислите интегралы методом замены переменной или подведением под знак дифференциала.
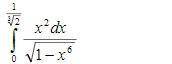
Другие вопросы по теме Математика
Популярные вопросы
- Почему звучит в сатире народная песня не шуми ты, мати зелена дубровушка...
2 - Https://www.facebook.com/TheProm2020WatchOnlineforFree...
2 - Як утворюється електромагнітна хвиля?...
2 - Решите задачу, записав вместе с дано и решение, типа того. Какова...
3 - Бесінші бөлімге дұрыс қойылған атауды анықта. Байжан мен Сәрсембайдың...
2 - • Проанализируйте эпизоды: - в штабе Кутузова;- в сражении при...
1 - Білеушелердің жанасу беттерінің аудандары бірдей. Қай білеуше үстелге...
2 - Kno3=kno2+o2 окислительно восстановительная реакция...
3 - На рисунке изображена шкала вольтметра. Каковы цена деления и предел...
1 - Как осуществляется порядок выполнения сложных физических упражнений...
3
Решим подведением под знак дифференциала: