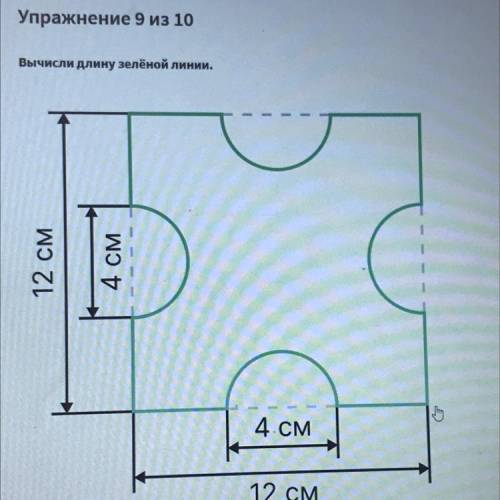
Вычислите длину зелёной линиии сторона 12 см
4 см

4+2=6
6+12=18
Ответ: 18

Чтобы решить эту задачу, нам понадобятся знания о теореме Пифагора и треугольниках.

1. Начнем с определения задачи. Нам нужно вычислить длину зеленой линии на картинке.

2. Обратимся к картинке и обозначим несколько важных величин. Пусть сторона внизу равна 12 см, а сторона влево равна 4 см.

3. Мы видим, что у нас имеется прямоугольный треугольник. Теорема Пифагора гласит, что квадрат гипотенузы (самой длинной стороны треугольника) равен сумме квадратов катетов (двух остальных сторон).

4. В нашем случае, гипотенуза - это зеленая линия, которую мы хотим вычислить. Катеты - сторона внизу (12 см) и сторона влево (4 см). Обозначим зеленую линию как "x".

Теперь мы можем записать уравнение с применением теоремы Пифагора:
x^2 = 12^2 + 4^2

5. Теперь произведем вычисления:
x^2 = 144 + 16
x^2 = 160

6. Чтобы найти x, возьмем квадратный корень из обеих сторон:
x = √160

7. Продолжим вычисления:
x ≈ √160
x ≈ 12.649

8. Таким образом, длина зеленой линии, округленная до двух десятичных знаков, составляет около 12.65 см.

Итак, ответ: Длина зеленой линии составляет около 12.65 см.