Вычислите
1) (64*4^-7)^2*(16-^1)^-3
2) 81^-3*27^-5/9^-12

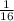1); 2)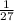

Пошаговое объяснение:

1)

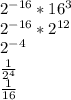
2)

Добрый день! Давайте посмотрим на каждый вопрос по отдельности.

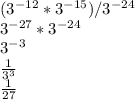
1) (64*4^(-7))^2*(16^(-1))^(-3)

Для начала упростим каждый из множителей в скобках:
• В первой скобке мы имеем произведение 64 и 4^(-7). Чтобы взять 4^(-7) внизу дроби, его можно записать как 1/4^7. Значит, (64*4^(-7)) можно переписать как 64*(1/4^7). Если мы упростим это выражение, получим 64*(1/16384) = 64/16384.
• Во второй скобке у нас 16^(-1). Здесь мы также можем взять 16^(-1) внизу дроби, записав его как 1/16. Значит, (16^(-1))^(-3) можно переписать как (1/16)^(-3). Если возвести 1/16 в степень -3, получим (1/16)^(-3) = (16/1)^3 = 16^3 = 4096.

Теперь мы можем записать итоговые значения для первого вопроса:
(64*4^(-7))^2*(16^(-1))^(-3) = (64/16384)^2*(1/16)^(-3) = (64^2/16384^2)*(16^3) = (4096/268435456)*4096 = 16777216/268435456.

2) 81^(-3)*27^(-5)/9^(-12)

Начнем с упрощения каждой дроби:
• 81^(-3) = (3^4)^(-3) = 3^(-12).
• 27^(-5) = (3^3)^(-5) = 3^(-15).
• 9^(-12) = (3^2)^(-12) = 3^(-24).

Теперь мы можем переписать исходное выражение с упрощенными дробями:
81^(-3)*27^(-5)/9^(-12) = 3^(-12)*3^(-15)/3^(-24).

После упрощения дробей мы можем применить свойство степени, которое говорит, что при делении степеней с одним и тем же основанием, мы вычитаем показатели степени:
3^(-12)*3^(-15)/3^(-24) = 3^(-12-15+24) = 3^(-3).

Итак, ответ для второго вопроса равен 3^(-3).

Надеюсь, я смог подробно и понятно объяснить решение этих математических задач. Если у вас возникнут еще вопросы, пожалуйста, не стесняйтесь задавать!