1. Математика
  2. Вычислить y и y для функции

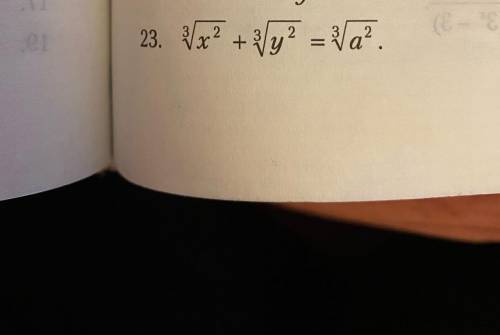
Вычислить y' и y'' для функции y(x) заданной неявно


Вычислить y' и y'' для функции y(x) заданной неявно

MrLinar MrLinar    1   15.01.2021 23:29    1

Ответы
полина2027 полина2027  14.02.2021 23:30

Пошаговое объяснение:

это функция заданная в неявном виде

F(x,y) = x^{2/3}+y^{2/3} -a^{2/3}\\

тогда производную ищем по формуле:

\frac{dy}{dx}=-\frac{F'_x}{F'_y}

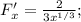
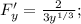
у нас         F'_x =\frac{2}{3x^{1/3} };     F'_y=\frac{2}{3y^{1/3}} ;

тогда первая производная

y'=\frac{dy}{dx} =-\frac{2}{3x^{1/3}} :\frac{2}{3y^{1/3}} =-\frac{y^{1/3}}{x^{1/3}}

вторая производная

\displaystyle y''=\left[\begin{array}{ccc}\bigg(\displaystyle \frac{u}{v}\bigg )'=\frac{u'v-uv'}{v2} \\\\\end{array}\right] =

=\displaystyle -\frac{\bigg ((1/3)y^{-2/3}y'\bigg )x^{1/3} -y^{1/3}\bigg((1/3)x^{-2/3}\bigg)}{x^{2/3}} =         (1)

теперь сюда вместо y' подставляем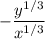 \displaystyle -\frac{y^{1/3}}{x^{1/3}}  и считаем эту всю мутотень

первая скобка числителя

\displaystyle \frac{1}{3y^{2/3} } *\bigg(-\frac{y^{1/3}}{x^{1/3}} \bigg )*x^{1/3} = -\frac{1}{3y^{1/3}}

вторая скобка числителя (ее берем сразу со знаком "-"

\displaystyle - \frac{y^{1/3}}{3x^{2/3}}

теперь -1/3 за скобки, а в скобках приводим к общему знаменателю

\displaystyle -\frac{1}{3}* \bigg( \frac{x^{2/3}+y^{2/3}}{y^{1/3}x^{2/3}} \bigg)

и теперь подставляем всё это в основную формулу (1) и получаем

y'' = -\bigg (- \displaystyle \frac{1}{3} *\frac{x^{2/3}+y^{2/3}}{x^{4/3}y^{1/3}} \bigg )=\frac{x^{2/3}+y^{2/3} }{3x \sqrt[3]{xy} }


Вычислить y' и y'' для функции y(x) заданной неявно
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
markinapolina19 markinapolina19  29.10.2020 10:08
Точка О лежит на отрезке АВ. Найдите длину отрезка ОВ, если длина отрезка АВ равна 320 мм, а длина отрезка АО равна 17см....
dilyaramazhitova dilyaramazhitova  29.10.2020 10:08
1. Задана пропорция x:6=30:у. Найдите значение ху реще​...
azizbekboboniyozov azizbekboboniyozov  29.10.2020 10:08
Перечислите все целые числа расположены между числами - 9.5 и - 43​...
ангел813 ангел813  29.10.2020 10:08
73 70 64 52 зандылыкты тап...
atsaruk2002 atsaruk2002  29.10.2020 10:08
Изобразите на координатной прямой точки А(4), В(10), С(-3). Найди длины отрезков АВ, АС, СВ, используя формулу...
diman211102 diman211102  29.10.2020 10:09
ЕГЭ2+2•100•100•100•1000000•9999999999•∞​...
В1и2к3т4о5р6и7я11 В1и2к3т4о5р6и7я11  29.10.2020 10:09
4. Диаметр окружности равен 6 м. Найдите длину окружности и площадь круга...
barbarask1 barbarask1  29.10.2020 10:09
Запеши в виде несократимой дроби 350/630 и 54/102​...
bokshitskayan bokshitskayan  29.10.2020 10:09
Вычисление площадей с интегралов...
anshul anshul  29.10.2020 10:09
Вычислить синус, косинус, тангенс, котангенс для данного аргумента t=315°​...

Популярные вопросы