Вычислить приближенное значение функции с использованием дифференциала .0.96^3 = (приближенно)

ответ: 0,88

Пошаговое объяснение:

Формула для приближенного вычисления значения функции в точке с дифференциала: f(x)=f(a+dx)≈f(a)+f'(a)dx

где x - заданная точка,

a - вс точка, в которой удобно вычислять значение функции и производной,

dx - разность между заданной точкой и вс

Ближайшая к 0,96 точка, где легко вычислить значение функции и ее производной, это 1 (в данном случае функция - ).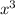

dx = x - a = 0,96 - 1 = -0,04

f(a) = f(1) = 1;

f'(x)=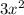

f'(a)=f'(1)=3;

f(x)=f(a+dx)≈f(a)+f'(a)dx:

f(0,96)≈1+3(-0,04)=0,88