Вычислить пределы, используя последствия первой и второй замечательных пределов и их последствия: 1) lim x->pi/2 (tg x/2)^(secx)
Другие вопросы по теме Математика
Популярные вопросы
- Сколько энергических слоев в атоме углерода?...
3 - Начертить прямую и обозначить ее строчной буквой. Отметить несколько точек...
3 - Алгебра повторение 7 класса эти 4 упражнения ...
2 - Напишите хронологию средневекового казахстана...
1 - Составьте текст инструкции о мерах безопасности в школе с учётом особенностей...
1 - күн ішінде дүкен 7/8 тонна картоп сатты, ал бірінші күні 1/4 тонна сатты....
1 - Какими свойствами обладают вещества с ионной связью...
2 - это биология я не понимаю...
3 - В электрочайнике неисправный нагреватель заменили на нагреватель вдвое...
2 - Начнем со словарно-орфографической работы. Подберите однокоренные слова:...
2
Неопределенность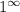 ⇒ применяется второй замечательный предел.
⇒ применяется второй замечательный предел.