Математика: Вычислить предел lim (d(n)/n) - где d(n), кол-во цифр числа n n- +беск

Вычислить предел lim (d(n)/n) - где d(n), кол-во цифр числа n
n->+беск

Ответы

razor200711 21.09.2021 11:00

$a_1=\frac{d(1)}{1}=1 a_2=\frac{d(2)}{2}=\frac{1}{2}a_3=\frac{1}{3}\ldots a_9=\frac{1}{9}\Rightarrow 0$

$a_{10}=\frac{d(10)}{10}=\frac{2}{10}a_{11}=\frac{2}{11}\ldots a_{99}=\frac{2}{99}\Rightarrow 0$

$a_{10^{n-1}}=\frac{d(10^{n-1})}{10^{n-1}}=\frac{n}{10^{n-1}}\ldots a_{10^n-1}=\frac{n}{10^n-1}\Rightarrow$

Последовательность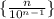 $\{\frac{n}{10^{n-1}}\}$ стремится к нулю, поэтому исходная последовательность стремится к нулю по лемме о "двух правоохранителях" (милиционерах, полицейских, жандармах, копах и т.д - в зависимости от страны и эпохи).

Доказать, что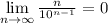 $\lim\limits_{n\to \infty}\frac{n}{10^{n-1}}=0$ можно многими (с правила Лопиталя, теоремы Штольца, бинома Ньютона, неравенства Бернулли - кто подскажет еще ?).

Например, бином Ньютона дает нам следующую оценку:

$10^{n-1}=(1+9)^{n-1}=1+9(n-1)+9^2\frac{(n-1)(n-2)}{2}+\ldots +9^{n-1}(n-1)(n-2)\Rightarrow$

Неравенство Бернулли применяем так:

$10^{n-1}=2^{n-1}\cdot 5^{n-1}=(1+1)^{n-1}\cdot 5^n\ge (1+(n-1)\cdot 1)\cdot 5^{n-1}=n\cdot 5^{n-1}\Rightarrow$

$\frac{n}{10^{n-1}}$

Лопиталь заменяет n на x, проверяет наличие неопределенности

$\left(\frac{\infty}{\infty}\right),$ вычисляет предел отношения производных:

$\lim\limits_{x\to+\infty}\frac{x'}{(10^{x-1})'}=\lim\frac{1}{10^{x-1}\cdot \ln 10}=0,$ и поскольку предел отношения производных существует и равен нулю, исходный предел также равен нулю.

Штольц не так хорошо известен, но наш предел вычисляет мгновенно. Однако я устал и (возможно) утомил читателя. Поэтому, памятуя Козьму Пруткова, заканчиваю.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика