1. Математика
  2. Вычислить площади фигур,

Вычислить площади фигур, ограниченных линиями, за-данными уравнениями в полярных координатах. P = 3cos2(фи)​

yoongiswag yoongiswag    3   04.07.2021 16:24    0

Ответы
Пирожочек07 Пирожочек07  03.08.2021 16:56

Пошаговое объяснение:

\displaystyle r=3cos(2\phi)

это полярная роза. поскольку аргумент для cos четный, то тут будет 4 лепестка.

из графика видим, что для половины лепестка аргумент изменяется

от 0 до п/4

нам надо найти площадь 1/2 лепестка и умножить ее на 8, т.е наша площадь будет

S= 8*S₁

площадь половины лепестка находим по формуле площади  криволинейного сектора

\displaystyle S_1=\frac{1}{2} \int\limits^{\phi_2}_{\phi_1} {r^2} \, d\phi

для нас будет (заметим, что при замене переменных для вычисления будут меняться и пределы интегрирования)

\displaystyle S_1=\frac{1}{2} \int\limits^{\pi/4}_0 {(3cos(2\phi))^2} \, d\phi =\frac{9}{2} \int\limits^{\pi/4}_0 {cos^2(2\phi)} \, d\phi=\left[\begin{array}{ccc}u=2\phi\quad du=2d\phi\\u_1=0\hfill\\u_2=\pi/2\hfill\end{array}\right] =

\displaystyle =\frac{9}{4} \int\limits^{\pi/2}_0 {\bigg (\frac{1}{2}cos(2u)+\frac{1}{2}\bigg ) } \, du =\frac{9}{8} \int\limits^{\pi/2}_0 {cos(2u)} \, du +\frac{9}{8} \int\limits^{\pi/2}_0 {} \, du=

\displaystyle =\frac{9}{8} \left[\begin{array}{ccc}s=2u\quad ds=2du\\s_1=0\hfill\\s_2=\pi\hfill\end{array}\right] +\frac{9u}{8} \bigg |_0^{\pi/2}=\frac{9}{16} \int\limits^\pi_0 {cos(s)} \, ds+\frac{9u}{8} \bigg |_0^{\pi/2}=

\displaystyle =\frac{9sin(s)}{16} \bigg |_0^\pi+\frac{9u}{8} \bigg |_0^{\pi/2}=0+\frac{9\pi}{16} =\frac{9\pi}{16}

итак, мы вычислили 1/2  лепестка розы. теперь узнаем всю площадь нашей полярной розы

\displaystyle S= 8*S_1 = 8*\frac{9\pi}{16} =\frac{9\pi}{2}

это и есть ответ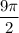   \displaystyle \frac{9\pi}{2}  условных единиц.


Вычислить площади фигур, ограниченных линиями, за-данными уравнениями в полярных координатах. P = 3c
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
gazizkadyrzhan gazizkadyrzhan  25.07.2019 19:00
Запиши множество делителей и множество кратных числа 17...
shm06 shm06  25.07.2019 19:00
Решите уравнение: 58164-х: 144=58141...
IrinaEfremova2003 IrinaEfremova2003  25.07.2019 19:00
Записать двузначные числа при умножении единиц которых на 7 применяется равенство 5×7=35...
нурбо1 нурбо1  25.07.2019 19:00
На все кашули пайшло 32 м тканины а на все сукенки 48 м расход тканины на кожны выбар был аднолькавы кольки кашуль и кольки сукенак пашыли кали сукенак пашыли на...
mixfix728 mixfix728  25.07.2019 19:00
От пристани отошёл теплоход со скорстью 18км/ч. через 2 часа вслед за ним отправился катер со скоростью 24км/ч. через сколько часов катер догонит теплоход?...
tkurchanova tkurchanova  25.07.2019 19:00
11 2/7 - 4 3/7 как решить напишите )...
flora21345 flora21345  25.07.2019 19:00
Составьте уравнения и найдите их корни сумма трёх слагаемых 97089 первое слагаемое 5674 второе 73478 чему ровна третье слагаемое...
tshaxzoda tshaxzoda  25.07.2019 19:00
Как записать уравнение (70-15)+x=81...
Asy209016 Asy209016  25.07.2019 19:00
Выполните действия умоляю 1) 3,5*4,2*4,1 2)1616,9: 95: 7,4...
AндрeйTh AндрeйTh  25.07.2019 19:00
Решить в детский сад 3 ящика апельсинов по 8 кг в каждой а мандаринов в 4 раза меньше сколько килограммов мандаринов в детский сад пишите действия...

Популярные вопросы