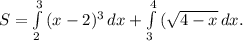Вычислить площади фигур, ограниченных линиями.

Даны 2 функци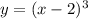и: и .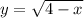

первая - кубическая парабола, сдвинутая на 2 единицы  в область положительных значений аргумента, функция возрастает,

вторая - ветвь параболы по оси Ох, функция убывает.

Это означает, что графики этих функций пересекаются внутри заданной области, фигура состоит из двух частей.

Находим крайние точки фигуры как точки пересечения с осью Ох при у = 0.

Правая точка. √(4 - x) = 0, возводим в квадрат обе части: х = 4.

Левая точка. (x - 2)^3 = 0, извлекаем кубический корень из обеих частей: х = 2.

Теперь находим точку пересечения: (x - 2)^3 = √(4 - x). Отсюда видно, что корень равен х = 3.

Теперь можно определить искомую площадь как сумму двух интегралов: