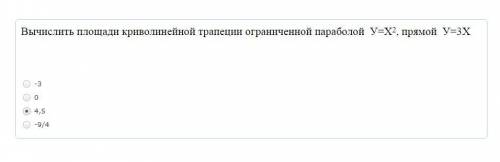
Вычислить площадь криволинейной трапеции
Другие вопросы по теме Математика
Популярные вопросы
- Вответ запишите наименьший положительный корень...
3 - Разобрать по составу слово железный, серебристый...
1 - Поздно вечером по местному радио передали прогноз погоды на следующий день. при...
3 - Представте что у маруси была своя кукла.какой диалог мог произойти между куклой...
2 - Скорость моторной лодки по течению реки 30 км/с в против течения 26 км/с найдите...
3 - Миша съел 9 вишен что состовляет одну четвертую всех вишен в вазе сколько ви...
1 - так вот, напишите слова с корнем вод . заранее тебе....
3 - На одной координатной плоскости постройте графики функций: 1) у=3х в квадрате...
2 - Ткань,находящаяся между древесиной и лубом. ....
1 - Чем занимались древнейшие жители эстонии?...
2
Пошаговое объяснение:
у₁ = 3х
у₂ = х²
найдем точки пересечения графиков
х²= 3х; х²-3х = 0; х(х-3) = 0; х₁ = 0; х₂ = 3
теперь посчитаем интеграл
ответ 4,5