вычислить площадь фигуры, ограниченной параболами и построить чертеж.
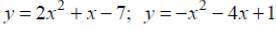
Другие вопросы по теме Математика
Популярные вопросы
- Площа паралелограма дорівнює 96 дм^2 ,периметр - 44 дм, а відстань...
3 - Физкультура 8. Кросс – это – а) Бег с ускорением б) Бег по искусственной...
2 - «Кладовой солнца» 1.Каким вы представляете рассказчика ОТВЕТЬТЕ...
1 - Вынеси общий множитель за скобки:11m(m−n)+8n(m−n). ...
3 - В заслонке, выполненной в форме квадрата со стороной 20 см, вырезали...
3 - 3. Для исправления ошибки в слове следует .а) щелкнуть на слове...
2 - По приведенным данным рассчитайте прибыль предприятия от продаж,...
1 - Решите уравнение: 13+3,2x+0,4x=40...
2 - Периметр равнобедренной трапеции равен 54 см. Боковая сторона...
3 - 1 маусым күніне эссе жазу керек...
3
Пошаговое объяснение:
y₁ = -x²-4x+1 ; y₂=2x² +x-7
находим точки пересечения
2x² +x-7 = -x²-4x+1 ⇒ 3x² +5x-8=0 ⇒ x₁ = -8/3; x₂=1
теперь найдем у₁ - у₂ = -x²-4x+1 -(2x² +x-7 ) = -3x² -5x+8
и теперь площадь фигуры