1. Математика
  2. Вычислить площадь фигуры ограниченной

Вычислить площадь фигуры ограниченной линиями y=x^2; y=2x; y=x

aydawgva aydawgva    3   18.09.2019 13:30    1

Ответы
Человек2029 Человек2029  08.10.2020 00:04
На участке от 0 до 1 функция ограничена сверху прямой у=2х,а снизу прямой у=х. На участке от 1 до 2 ограничена сверху прямойу=2х,а снизу параболой.
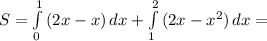
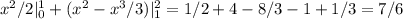
S= \int\limits^1_0 {(2x-x)} \, dx + \int\limits^2_1 {(2x-x^2)} \, dx =x^2/2|^1_0+(x^2-x^3/3)|^2_1=1/2+4-8/3-1+1/3=7/6
ПОКАЗАТЬ ОТВЕТЫ
nari06 nari06  08.10.2020 00:04
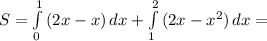
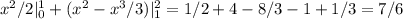
1234456+656789-68988=
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
envoyfromhell envoyfromhell  11.01.2021 20:39
6. Фермер потратил 260 евро на 325 доз вакцины для своего скота. Сколько вы должны потратить, даже если вам нужно купить еще 180 доз?​...
adadasda65p06utn adadasda65p06utn  11.01.2021 20:39
решить задачу В столовую привезли 2580 кг сахара.В каждый день использовали по 75 кг сахара. Сколько сахара осталось после 22 дней ?...
mashabanan15 mashabanan15  11.01.2021 20:39
12a + 2d-4= 1 7x-2xt 5x+10= решить уровнение...
smokeech smokeech  11.01.2021 20:38
Какие две одинаковые числа умножили друг друга получилось =8...
aigylka764 aigylka764  11.01.2021 20:38
Длина окружности равна 107,514 см. Значение числа π≈3,14. Определи радиус данной окружности (с точностью до сотых):R = см. разобраться...
exii exii  11.01.2021 20:36
Соседние стороны квадрата и прямоугольника перпендикулярны друг другу Продемонстрируйте данное утверждение при рисунка...
mitaikooo mitaikooo  11.01.2021 20:36
с математикой! Несколько примеров хотябы! Даю все свои Больше нету....
Астар Астар  30.04.2021 10:02
Знайдіть число, якщо3/4 цього числа дорівнює 7,5​...
saidislom01 saidislom01  30.04.2021 10:01
Запишите точки (рис. 8.6),которые: 1)принадлежат окружности 2)принадлежат кругу 3)не пренадлежат кругу....
GgEz11134 GgEz11134  30.04.2021 10:01
Пример: -(-476)-349+430= С решением...

Популярные вопросы