Вычислить площадь фигуры ограниченной линиями y= -x^2+6x И y=2x+3
Другие вопросы по теме Математика
Популярные вопросы
- В отборе корней можно ли одну точку записать по разному? С ответом не сошлось,...
1 - Запишите условия задачи в виде дано найти Определите массу Na2CO3 • 10 Н2О (кристаллической...
3 - Створення сайту засобами системи керування вмістом веб-сайтів. Етапи розробки...
1 - Выполните полный синтаксический разбор с описанием типов предложений и объясните...
1 - по теме: Світ юридичних професій по теме: Світ юридичних професій.7. 8.10. >...
1 - Визначте, який прогноз народження хворих на дальтонізм дітей, якщо батько хворий...
2 - Предложения, которыеCOOTRETCTBYT KOMHateBbioepute orker:There is a chair in front...
2 - Обчисліть та позначте об єм водню (н.у.), який потрібен для гідрування олеїнової...
1 - 13/28. (если не трудно то с решением)...
2 - Общество в целом, отдельные классы, социальные слои и организации смотрят на...
3
Приравняем данные функции и решим полученное уравнение:
Теперь находим определённый интеграл. Это и будет ответом.
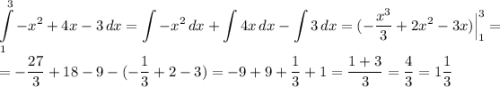
ответ: