Вычислить площадь фигуры ограниченной линиями y=x^2+2x+3 x=0 x=-3 y=0
Другие вопросы по теме Математика
Популярные вопросы
- Опишите образ эраста в повести бедная лиза...
2 - Впрямоугольном параллелепипеде высота 5 с, объем 105см3. найдите объем...
2 - Реши разными из двух городов навстречу друг другу выехали одновременно...
1 - Вставить правильные предлоги. 1. he asked an expensive pair of shoes....
2 - Сауыншы составить пятистишие 1) слово 2) два прилагательных 3) три глагола...
2 - Дано число n. написать программу, выводящую на экран сумму квадратов...
2 - Решить уровнение x*4=28+12 никак решить?...
2 - Выберите строку, в которой все выделенные буквы являются проверяемой...
2 - Дроби к наименьшему общему знаменателю 7/20и1/15 8/11и5/8 3/22и2/33...
3 - Zn(oh)2 + h3bio4 сколько солей может быть образовано...
3
Вспомним формулу Ньютона-Лейбница:
Подставим численные значения в формулу и найдём определённый интеграл:
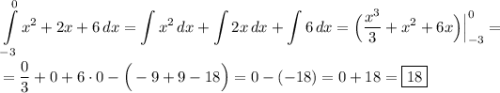
ответ: