Вычислить площадь фигуры,ограниченной линиями y^2-4x=0,x-y=0
Ответы
Здесь лучше составить интеграл относительно переменной у.
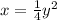 и
и 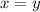
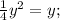
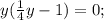
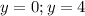 -пределы интегрирования
-пределы интегрирования
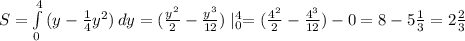
ПОКАЗАТЬ ОТВЕТЫ
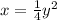 и
и 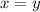
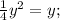
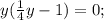
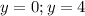 -пределы интегрирования
-пределы интегрирования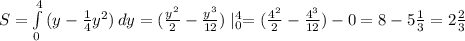
Другие вопросы по теме Математика
Популярные вопросы
- Как перевести на язык слово is he cute? и как ответить на языке...
2 - Подскажите как решить уравнения 2×=9+×...
2 - Ходасевич владислав фелицианович и поэту анализ стихотворения...
3 - Сколько простых делителей имеет число m = 3×4×5? a) 3 . b ) 4 c ) 5 d)...
1 - Машины выехали из двух городов одновременно навстречу друг другу и встретились...
3 - Complete the sentences with some or any, is or are. 1) _ there_ cheese?...
3 - Что привозили в северное причерноморье и что вывозили? (заранее )...
1 - Длинна прямоугольного поля 300м а ширина 200м найти площадь поля выразить...
2 - Тест на тему «вставные конструкции». найдите неверное утверждение. а) вводные...
3 - Напишите 10 предложений з to be (5 предложений отрицательных и 5 положительных)...
1