Вычислить площадь фигуры, ограниченной линиями: у = - x2 + 4 и у = 0
Другие вопросы по теме Математика
Популярные вопросы
- Объясните понятие подтекст в маленьком принце....
2 - Всё то. чего коснётся человек, приобретает нечто человечье разобрать нечто...
2 - Итак , я вам вопросик. зыс- это this ( я так это буду называть=)зыс)) зэт...
1 - Кшару незаряженного электроскопа поднесли положительно заряженную стекл....
1 - Нужна знайдіть суму перших трьох членів арифметичної прогресії(an)якщо a1=8,d=12...
2 - Кого вы можете назвать великим человеком 17-18 века, которого вы запомнили....
1 - 7предложений с главными второстепенными членами предложениями ну решить некак...
2 - Придумайте 2-3 вопроса для викторины о франции и великобретании...
3 - 1. участникам олимпиады от марсиан записано с всех символов марсианского...
1 - Площадь занимает на колхозном поле посадкой клубники 50880 квадратных метров...
3
Приравняем данные функции и решим полученное квадратное уравнение.
По теореме Ньютона-Лейбница найдём площадь данной фигуры.
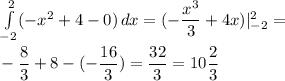
ответ: