Вычислить площадь фигуры, ограниченной линиями
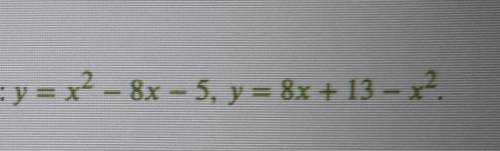
Другие вопросы по теме Математика
Популярные вопросы
- Назовите главный предмет литературы и искусства....
1 - Польский историк Л. Кубала сравнивал Б. Хмельницкого с предводителем Английской...
3 - Исполнитель Робот действует в следующей обстановке: Для Робота составлена следующая...
3 - Сразы дам 5. Звезд(人 •͈ᴗ•͈)(✷‿✷)...
1 - Что саки ставили превыше всего, отвечая перситскому послу...
2 - Про ПыеПроаерано през аеро аксе дрзатоалих Дія Победы над галтерской Геразпрей...
3 - Вычисли, записывая по действиям (90 050-219×380+190): 90(302 281-12 649): 48+3...
1 - Зробіть синтаксичний розбір речення У навстіж розчинений простір, де квіти і трави...
2 - г) Урожайность болгарского перца, собранного одним ферме-ром с поля площадью 3...
2 - Көде қайда өседіҚандай гулдері бар қалай пайдаланылады...
1
Пошаговое объяснение:
найдем точки пересечения парабол
х²-8х-5=8х+13-х²
2х²-16х-18=0
х²-8х-9=0
х₁ ₂ =(8±√(64+36))/2
х₁ =(8-10)/2 х₂ =(8+10)/2
х₁ =-1 х₂ =9
проверим какая парабола выше,подставив 0 из области в параболы.
у=х²-8х-5 у=-5 при х=0
у=8х+13-х² у=+13 при х=0
значит , чтобы найти площадь в интеграле будем от второй отнимать первую( От той,что выше отнимаем нижнюю)
∫₋₁⁹((8х+13-х²)-(х²-8х-5))d(x)=
∫₋₁⁹(8х+13-х²-х²+8х+5)d(x)=
∫₋₁⁹(16х+18-2х²)d(x)= (16x²/2+18x-2x³/3)₋₁⁹=
(16*81/2+18*9-2*729/3) -(16*1/2+18*(-1)-2*(-1)/3)=
648+162-486-8+18+2/3=334 2/3