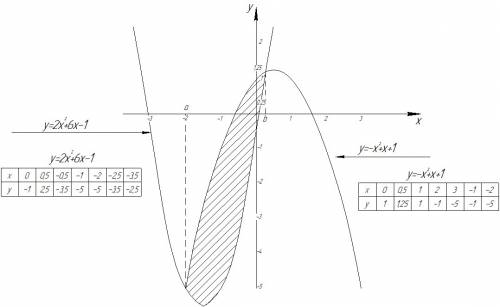
Вычислить площадь фигуры, ограниченной линиями:
Ответы
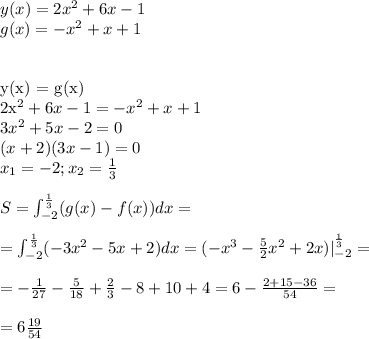
Найдем абсциссы точек пересечения заданных линий:
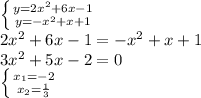
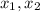 - пределы интегрирования. (на рисунке изображены как "a" и "b".
- пределы интегрирования. (на рисунке изображены как "a" и "b".
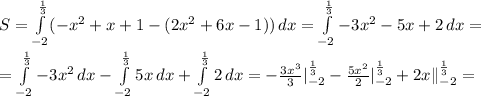
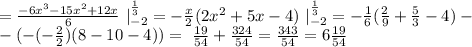
ПОКАЗАТЬ ОТВЕТЫ
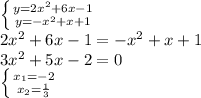
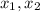 - пределы интегрирования. (на рисунке изображены как "a" и "b".
- пределы интегрирования. (на рисунке изображены как "a" и "b".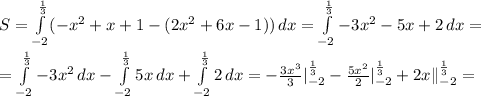
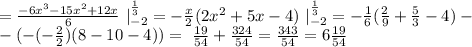

Другие вопросы по теме Математика
Популярные вопросы
- СОЧ идёт Первый член арифметической прогрессии равен 3, а знаменатель равен 4....
3 - напишите правду а не што прихоодит в голоову этоо всё чтоо уменя есть негізгі...
3 - Сына суреттен сурек кабатынын боялу себебын аныктаныз....
1 - Определите тип дыхания птиц( ...
1 - Для последовательности 2;3/8,4/27;5/64;...составить формулу n-го члена an....
3 - Ақиқат жалған және берілмеген ақпаратты анықтаплз...
3 - Найдите сложное предложение (Знаки препинания внутри предложения не расставлены)...
1 - Рассчитать приблизительный объём 36% раствора хлоридной кислоты, необходимый для...
2 - 1. Match the words in Column A to the words in Column B 1. digitalA. dome2. virtualB....
1 - 1) 4/7(-14a + 7x) - 8/11(+223 + 11)2) -2,5(10a - 1) + 3,8(5a – 3); У меня сссч...
1