Вычислить определители приведением к треугольному виду

dimapm04 2 30.12.2021 21:27 1

Question

Математика: Вычислить определители приведением к треугольному виду

dimapm04 · Answer

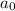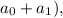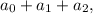Вынесем из всех строчек, кроме первой, множитель x, после чего прибавим к первой строчке вторую, умноженную на a_0 (в результате в первой строчке на первом месте появится ноль, а на втором месте будет стоять a_0+a_1), после чего к первой строчке прибавим третью, умноженную на a_0+a_1, четвертую, умноженную на a_0+a_1+a_2, и так далее, последнюю, умноженную на 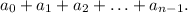$a_0+a_1+a_2+\ldots+a_{n-1}.$ Получаем

$x^n\cdot\begin{vmatrix}0&0&0&\ldots&0&a_0+a_1+\ldots+a_n\\-1&1&0&\ldots& 0&0\\0&-1&1&\ldots &0&0\\\hdotsfor{6}\\0&0&0&\ldots&-1&1\end{vmatrix}.$

Остается разложить получившийся определитель по первой строчке, после чего получается нижнетреугольная матрица, равная произведению диагональных элементов (а на диагонали стоят единицы).

В результате получается такой ответ:

$(-1)^{n+2}\sum\limits_{i=0}^na_i \cdot x^n.$