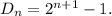Вычислить определители методом рекуррентных соотношений

Обозначим этот определитель через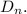 Раскладывая его по первой строке, получаем

(последнее равенство получено с разложения по первому столбцу). Конечно, в этом равенстве предполагается, что n>2.

Непосредственно ищем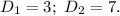 используя выведенную формулу, находим 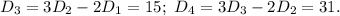Замечаем такую закономерность:

Естественно возникает гипотеза, что для любого натурального n

Докажем это. Для начальных значений n гипотеза уже проверена, остается проверить индукционный переход. А именно, предположив, что гипотеза верна при n=k и n=k+1, докажем, что тогда она верна и при n=k+2. В самом деле,

Тем самым гипотеза доказана при всех натуральных  n.

Замечание. Задачу можно было бы решить с характеристического уравнения, но в этом случае пришлось бы слишком много объяснять.

ответ: