1. Математика
  2. Вычислить определенный интеграл

Вычислить определенный интеграл по формуле ньютона-лейбница: 1) интеграл от 0 до pi ∫cos^2xdx; 2) интеграл от 0 до 1 ∫x^2e^x^2dx

annshirokikh annshirokikh    3   30.08.2019 12:40    0

Ответы
elenaignashova1 elenaignashova1  03.08.2020 12:05
Так как условие второго непонятно, выкладывается только первый интеграл:
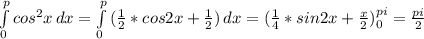
\int\limits^p_0 { cos^{2}x } \, dx = \int\limits^p_0 {( \frac{1}{2}*cos 2x+ \frac{1}{2} )} \, dx = ( \frac{1}{4} *sin2x+ \frac{x}{2} )_0^{pi}= \frac{pi}{2}
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
принцеска005 принцеска005  19.01.2021 08:58
Бөлінгіштерді тиімді қосылғыштарға жіктеу үшін, әр бояу ыдысына тиісті қылқаламды таңда....
mullyminovam mullyminovam  19.01.2021 08:57
Задачи на совместную работу. Урок 4 На ремонте дороги работали 15 человек, они должны были закончить работу за 12 дней. Утром на пятый день прибыло еще несколько...
y2334455 y2334455  19.01.2021 08:57
Задание 1. 3.4x-4-4,8-х95+2=57-56Задание 2.4-9=3(x-43(2x-9)=5(x-4)​...
ivanovartem02 ivanovartem02  19.01.2021 08:57
Бырлесып орындалатын жұмыстарға катысты. Есептер 4-сабак помагите...
cvetaharlanova5 cvetaharlanova5  19.01.2021 08:57
Биология 6 класс параграф 28 дыхание растений питанипе обмен веществ в растениях...
shydik37 shydik37  19.01.2021 08:57
4 1 5 1. Есептеңіз: 8--2- 4 16 ) , 25 5 А) 32 1 B) 16 19 C) 20 17 D) 25...
shahmir2406 shahmir2406  19.01.2021 08:56
Построить прямую 4x-7y+28=0 приведя его к виду уравнения прямой в отрезках...
lol1337rus lol1337rus  19.01.2021 08:56
Есепті шығар. Мотоциклшілердің арақашықтығы - 50 км. Біріншісі - 40км/сағ, екінші 50 км/сағ жылдамдықпен қозғалды. Қанша уақыттан кейін екіншісі біріншісін қуып...
Mysicista Mysicista  19.01.2021 08:55
В загородный лагерь необходимо вывезти 150 человек. Какое наименьшее количество автобусов надо заказать, если вместимость автобуса 42 пассажира а) 4 б)6 в)7...
матькорейцев2345 матькорейцев2345  19.01.2021 08:55
Сторона первого квадрата на 5 см меньше стороны второго Квадрата, а площадь второго квадрата на 45 см большеПлощади первого квадрата. Найди сторону первого квадрата.Land​...

Популярные вопросы