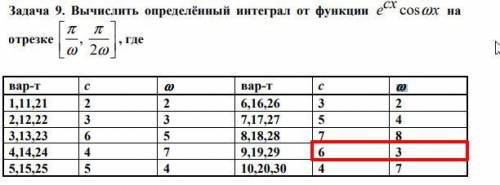
Вычислить определённый интеграл от функции
Другие вопросы по теме Математика
Популярные вопросы
- Анализ стиха Блока Летний вечер по плану. 1) Какими чувствами...
1 - Настроение стихотворения Я покинул родимый дом...
2 - 1 фото Представте в виде многочлена выражения 2 фотозапишите...
3 - Большее боковое ребро трапеции наклонено к основанию под углом...
1 - От куска ткани длиной 18 метров каждый день отрезают по 3 метра.Через...
1 - Училка имела ввиду что нужно уровнением а не таким образом...
2 - Где нельзя хранить товар? 1 рядом с трубами, 2 рядом с входной...
1 - Написати текст про лондонське око...
1 - Без граматичної помилки є відповідь на запитання Котра година?...
2 - решить с обьяснениями 5/6*(1/2x-2/3)=3x-2 1/4...
1
Пошаговое объяснение:
здесь получится рекурсивный интеграл. поэтому сначала решаем неопределенный интеграл
схема такая: два раза будем интегрировать по частям
формула интегрирования по частям
итак, первый раз
f = cos(3x) ⇒ f' = -3sin(3x)
g'= e⁶ˣ ⇒ g = (e⁶ˣ )/6
тогда
теперь второй раз интегрируем получившийся справа интеграл
f = -3sin(3x) ⇒ f' = -9cos(3x)
g' = (e⁶ˣ )/6 ⇒ g = (e⁶ˣ )/36
тогда
или
вот, мы видим, что исходный интеграл повторился. теперь у нас вроде как уравнение относительно этого интеграла. решим его и получим
теперь осталось только подставить пределы интегрирования
всё. это ответ