Вычислить определенные интегралы по формуле Ньютона – Лейбница
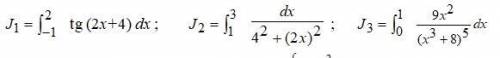
Другие вопросы по теме Математика
Популярные вопросы
- Мәтінде берілген ақпаратты аңықтаңыз...
2 - Сор Соч поомшите посмотрите в ссылке...
3 - НЕ ЗНАЮ не знаю не знаю очень дизайн - создания вещей промышленным или руками...
1 - Какие племена расселились с 11-13 веках на обширных территориях от Дуная до...
3 - НУ ЗАДАНИЕ В ПРОФИЛЕ ПРО ДУБРОВСКОГО, 4 ЧАСА ОСТАЛОСЬ, АААААААААА ЛАЙКНУ, ОТМЕЧУ...
3 - Сравните природную экосистему и агроэкосистему на примере разнотравного луга...
2 - Дано выражение x^2– 12х+35. а) Запишите данное выражение в виде (х - а)^2+b....
1 - Быз концертке дайындаламыз...
2 - Третій уточнений Закон И.Кеплера використовується в основному для визначення......
2 - Смесь циклогексена и водорода, с мольным соотношением компонентов 1:5, пропустили...
2
Пошаговое объяснение:
1)
2)
3)