Вычислить определенные интегралы:
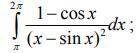
Другие вопросы по теме Математика
Популярные вопросы
- Различите с реакций соединения: пентан, пентен-1, пентин-1, пентин-2, пентадиен-1,3....
1 - Составить 4 предложения на правописание не с глаголами и 4 предложения на правописание...
3 - Особенности полового размножения растений? заранее...
2 - Кто такой гордиев узел и какую роль он сыграл в жизни александра ( 20 )...
3 - Cкакими трудностями сталкивался человек в ранее новое время ?...
2 - Таблиця взаємні права та обов язки батьків і дітей , в то нас...
3 - Правда много написать сочинение максим горький детство заранее ...
3 - 1) скільки грамів cao утворюється при згоряні 2 грамів ca? 2) об ясніть масу...
1 - Разложить на множители а в четвертой степени минус а 3 степени плюс а минус...
1 - Пересказ произведения «солнце в аистовом гнезде»...
3
Пошаговое объяснение: