1. Математика
  2. Вычислить объёмы тел, ограниченных

Вычислить объёмы тел, ограниченных поверхностями: z=9-x^2-y^2 ,z=0

катя4770 катя4770    3   15.09.2019 13:30    1

Ответы
Kurlyk111 Kurlyk111  01.09.2020 14:24

z=9-x^2-y^2 - эллиптический параболоид, полученный отражением параболоида z=x^2+y^2 относительно xOy и последующего за этим сдвига на 9 единиц вдоль положительного направления Oz. В сечении плоскостью z=z_0 получаем окружность 9-z_0=x^2+y^2 радиуса \sqrt{9-z_0}.

z=0 - плоскость, совпадающая с плоскостью xOy.

Поверхности пересекаются по уравнению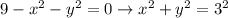 9-x^2-y^2=0\to x^2+y^2=3^2 - окружности радиуса 3 и центром в начале координат.

Пределы по y: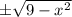 \pm \sqrt{9-x^2}, по x: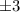 \pm 3

Вычисление интеграла в приложении.


Вычислить объёмы тел, ограниченных поверхностями: z=9-x^2-y^2 ,z=0
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
aruzhanormanova aruzhanormanova  25.05.2019 05:50
Вцентре, имеющего квадратную форму, разбита цветочная клумба, которая также имеет форму квадрата.площадь участка равна 100 кв.м. сторона клумбы в 2 раза меньше стороны...
lina5555555 lina5555555  25.05.2019 05:50
Содной и той же станции в одно и тоже время вышли в противоположных направлениях два поезда . скорость одного поезда 50км/ч , а другого 85км/ч. какое расстояние будет...
Bibi123456 Bibi123456  25.05.2019 05:50
Выполните действие: 5/12-2/9= 5/9+3/4=...
артур614 артур614  25.05.2019 05:50
Сплавлено 2 слитка золота 84-й и 64-й пробы и получено 50 г золота 76-й пробы. сколько весил каждый из сплавленных слитков?...
baandas baandas  25.05.2019 05:50
Характерные деревья в тайге окр мир...
MAKCUMKA228 MAKCUMKA228  25.05.2019 05:50
Когда мы идём из леса, от которого до деревни 2 километра, на полпути нас встречает бабушкин пёс дружок. он бежит в 10 раз быстрее, чем мыидём. это непоседливая собака,...
savkinaveronika savkinaveronika  25.05.2019 05:50
1) кратность числа x: x, 22, 33, ; 2) кратность числа y: y, 18, 27, ; 3) кратность числа m: m, 26, 39, ; 4) кратность числа n: n, 30, 45, ; здесь x, y, m и n какие...
kurtenokalina2 kurtenokalina2  25.05.2019 05:50
Нужен доклад живая природа осени 2 класс...
TopGmaer TopGmaer  25.05.2019 05:50
Выражение а) 3а+5а б) 7b-4b в)2d+7d-3 г)12+6c+c...
hfdsgbgc hfdsgbgc  25.05.2019 05:50
Замените данное число процентов обыкновенной дробью со знаменателем 100, а затем сократите эту дробь на наибольший общий делитель её числителя и знаменателя: 75%= 20%=...

Популярные вопросы