1. Математика
  2. Вычислить объем тела v

Вычислить объем тела v ограниченного поверхностями
\begin{cases}2z = {x}^{2} + {y}^{2} \\ y + z = 4 \end{cases}
плотность тела v считать равной 1.
( нужно выполнить с двойного интеграла)​

Семён3228 Семён3228    2   21.09.2019 11:30    0

Ответы
zhenya4546 zhenya4546  08.10.2020 07:01

z=\dfrac{x^2+y^2}{2} - эллиптический параболоид. В сечении z=z_0, параллельном плоскости xОy, получаем окружность с радиусом \sqrt{2z_0} и центром в начале координат.

z=4-y - плоскость, параллельная оси Ox. В сечении z=z_0, параллельном xOy получаем прямую y=4-z_0.

Найдем, где графики пересекаются, приравняв их уравнения: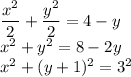 \dfrac{x^2}{2}+\dfrac{y^2}{2}=4-y\\ x^2+y^2=8-2y\\ x^2+(y+1)^2=3^2

В проекции на xOy получаем окружность радиуса 3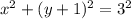 x^2+(y+1)^2=3^2. Пределы по x будут 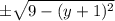\pm \sqrt{9-(y+1)^2}, по y будут 3-1=2 и -3-1=-4.

Вычисление интеграла в приложении.


Вычислить объем тела v ограниченного поверхностями [tex]\begin{cases}2z = {x}^{2} + {y}^{2} \\ y + z
Вычислить объем тела v ограниченного поверхностями [tex]\begin{cases}2z = {x}^{2} + {y}^{2} \\ y + z
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Андрей22111111 Андрей22111111  21.05.2020 15:59
Запишіть рівняння дотичної до графіку функції y=x^2-2x у точні з абсцисою x0=1...
Annkot22 Annkot22  21.05.2020 15:59
(1+7/23)×(2-4/25):(99-981/5)=​...
попкорн6 попкорн6  21.05.2020 15:59
Найдите сумму степенного ряда:...
nikysa1 nikysa1  21.05.2020 15:59
решить. Замечательные пределы...
artyom11111112 artyom11111112  21.05.2020 15:59
1з двох міст, відстань між якими 336 км, одночасно на зустріч один одному, виіхали мотоцикліст і велосипедист. Швидкість велосипедиста 15 км/год, а мотоцикліста-на 12 км/год...
alyonasmirnova5 alyonasmirnova5  21.05.2020 15:59
контрольная через 40 мин здавать...
polaykovaz polaykovaz  21.05.2020 16:00
E И B Н о a н B 3 с A Ы й * E ш w I a р A 3 у K Г Я ч у Я a Б у у у p Выталкивающая сила, действующая со стороны воды и воздуха, – Самый первый воздухоплавательный аппарат —...
maly2111q maly2111q  21.05.2020 16:00
Мотоцикліст і велосипедист їдуть назустріч одинодному. Зараз відстань між ними 272 км. Через скількигодин вони зустрінуться, якщо швидкість велосипедиста12 км/год., а швидкість...
Jessicacoen Jessicacoen  01.06.2020 10:47
Найдите объём правильной четырёхугольной пирамиды, если сторона основания равна 6 см, а высота пирамиды 4 см....
555766 555766  01.06.2020 10:47
1)найдите радиусы окружностей описанной вокруг треугольника и вписаной в треугольник если известны стороны тереугольника а)4 13 15 б)4 5 7 2)диогонали паралелограмма равны 10...

Популярные вопросы